Terence Tao facts for kids
Quick facts for kids
Terence Tao
FAA FRS
|
|
|---|---|
 |
|
| Born | 17 July 1975 Adelaide, South Australia, Australia
|
| Citizenship |
|
| Alma mater |
|
| Known for | Partial differential equations, analytic number theory, random matrices, compressed sensing, combinatorics, dynamical systems |
| Spouse(s) | Laura Tao |
| Children | 2 |
| Awards | Fields Medal (2006)
List
Salem Prize (2000)
Bôcher Memorial Prize (2002) Clay Research Award (2003) Australian Mathematical Society Medal (2005) Ostrowski Prize (2005) Levi L. Conant Prize (2005) MacArthur Award (2006) SASTRA Ramanujan Prize (2006) Sloan Fellowship (2006) Fellow of the Royal Society (2007) Alan T. Waterman Award (2008) Onsager Medal (2008) King Faisal International Prize (2010) Nemmers Prize in Mathematics (2010) Pólya Prize (2010) Crafoord Prize (2012) Simons Investigator (2012) Breakthrough Prize in Mathematics (2014) Royal Medal (2014) PROSE Award (2015) Riemann Prize (2019) Princess of Asturias Award (2020) Bolyai Prize (2020) IEEE Jack S. Kilby Signal Processing Medal (2021) Global Australian of the Year Award (2022) Grande Médaille (2023) Best Paper Award (2023) Alexanderson Award (2023) |
| Scientific career | |
| Fields | Harmonic analysis |
| Institutions | University of California, Los Angeles |
| Thesis | Three Regularity Results in Harmonic Analysis (1996) |
| Doctoral advisor | Elias M. Stein |
| Doctoral students | Monica Vișan |
| Terence Tao | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Traditional Chinese | 陶哲軒 | ||||||||||||||||||
| Simplified Chinese | 陶哲轩 | ||||||||||||||||||
|
|||||||||||||||||||
Terence Chi-Shen Tao FAA FRS (Chinese: 陶哲軒; born 17 July 1975) is an Australian-American mathematician, Fields medalist, and professor of mathematics at the University of California, Los Angeles (UCLA), where he holds the James and Carol Collins Chair in the College of Letters and Sciences. His research includes topics in harmonic analysis, partial differential equations, algebraic combinatorics, arithmetic combinatorics, geometric combinatorics, probability theory, compressed sensing and analytic number theory.
Tao was born to Chinese immigrant parents and raised in Adelaide. Tao won the Fields Medal in 2006 and won the Royal Medal and Breakthrough Prize in Mathematics in 2014, and is a 2006 MacArthur Fellow. Tao has been the author or co-author of over three hundred research papers, and is widely regarded as one of the greatest living mathematicians.
Contents
Life and career
Family
Tao's parents are first generation immigrants from Hong Kong to Australia. Tao's father, Billy Tao, was a Chinese paediatrician who was born in Shanghai and earned his medical degree (MBBS) from the University of Hong Kong in 1969. Tao's mother, Grace Leong, was born in Hong Kong; she received a first-class honours degree in mathematics and physics at the University of Hong Kong. She was a secondary school teacher of mathematics and physics in Hong Kong. Billy and Grace met as students at the University of Hong Kong. They then emigrated from Hong Kong to Australia in 1972.
Tao also has two brothers, Trevor and Nigel, who are currently living in Australia. Both formerly represented Australia at the International Mathematical Olympiad. Furthermore, Trevor Tao has been representing Australia internationally in chess and holds the title of Chess International Master.
Tao speaks Cantonese but cannot write Chinese. Tao is married to Laura Tao, an electrical engineer at NASA's Jet Propulsion Laboratory. They live in Los Angeles, California, and have two children.
Childhood
A child prodigy, Terence Tao skipped 5 grades. Tao exhibited extraordinary mathematical abilities from an early age, attending university-level mathematics courses at the age of 9. He is one of only three children in the history of the Johns Hopkins Study of Exceptional Talent program to have achieved a score of 700 or greater on the SAT math section while just eight years old; Tao scored a 760. Julian Stanley, Director of the Study of Mathematically Precocious Youth, stated that Tao had the greatest mathematical reasoning ability he had found in years of intensive searching.
Tao was the youngest participant to date in the International Mathematical Olympiad, first competing at the age of ten; in 1986, 1987, and 1988, he won a bronze, silver, and gold medal, respectively. Tao remains the youngest winner of each of the three medals in the Olympiad's history, having won the gold medal at the age of 13 in 1988.
Career
At age 14, Tao attended the Research Science Institute, a summer program for secondary students. In 1991, he received his bachelor's and master's degrees at the age of 16 from Flinders University under the direction of Garth Gaudry. In 1992, he won a postgraduate Fulbright Scholarship to undertake research in mathematics at Princeton University in the United States. From 1992 to 1996, Tao was a graduate student at Princeton University under the direction of Elias Stein, receiving his PhD at the age of 21. In 1996, he joined the faculty of the University of California, Los Angeles. In 1999, when he was 24, he was promoted to full professor at UCLA and remains the youngest person ever appointed to that rank by the institution.
He is known for his collaborative mindset; by 2006, Tao had worked with over 30 others in his discoveries, reaching 68 co-authors by October 2015.
Tao has had a particularly extensive collaboration with British mathematician Ben J. Green; together they proved the Green–Tao theorem, which is well known among both amateur and professional mathematicians. This theorem states that there are arbitrarily long arithmetic progressions of prime numbers. The New York Times described it this way:
In 2004, Dr. Tao, along with Ben Green, a mathematician now at the University of Cambridge in England, solved a problem related to the Twin Prime Conjecture by looking at prime number progressions—series of numbers equally spaced. (For example, 3, 7 and 11 constitute a progression of prime numbers with a spacing of 4; the next number in the sequence, 15, is not prime.) Dr. Tao and Dr. Green proved that it is always possible to find, somewhere in the infinity of integers, a progression of prime numbers of equal spacing and any length.
Many other results of Tao have received mainstream attention in the scientific press, including:
- his establishment of finite time blowup for a modification of the Navier–Stokes existence and smoothness Millennium Problem
- his 2015 resolution of the Erdős discrepancy problem, which used entropy estimates within analytic number theory
- his 2019 progress on the Collatz conjecture, in which he proved the probabilistic claim that almost all Collatz orbits attain almost bounded values.
Tao has also resolved or made progress on a number of conjectures. In 2012, Green and Tao announced proofs of the conjectured "orchard-planting problem," which asks for the maximum number of lines through exactly 3 points in a set of n points in the plane, not all on a line. In 2018, with Brad Rodgers, Tao showed that the de Bruijn–Newman constant, the nonpositivity of which is equivalent to the Riemann hypothesis, is nonnegative. In 2020, Tao proved Sendov's conjecture, concerning the locations of the roots and critical points of a complex polynomial, in the special case of polynomials with sufficiently high degree.
Recognition
Tao has won numerous mathematician honours and awards over the years. He is a Fellow of the Royal Society, the Australian Academy of Science (Corresponding Member), the National Academy of Sciences (Foreign member), the American Academy of Arts and Sciences, the American Philosophical Society, and the American Mathematical Society. In 2006 he received the Fields Medal; he was the first Australian, the first UCLA faculty member, and one of the youngest mathematicians to receive the award. He was also awarded the MacArthur Fellowship. He has been featured in The New York Times, CNN, USA Today, Popular Science, and many other media outlets. In 2014, Tao received a CTY Distinguished Alumni Honor from Johns Hopkins Center for Gifted and Talented Youth in front of 979 attendees in 8th and 9th grade that are in the same program from which Tao graduated. In 2021, President Joe Biden announced Tao had been selected as one of 30 members of his President's Council of Advisors on Science and Technology, a body bringing together America's most distinguished leaders in science and technology. In 2021, Tao was awarded the Riemann Prize Week as recipient of the inaugural Riemann Prize 2019 by the Riemann International School of Mathematics at the University of Insubria. Tao was a finalist to become Australian of the Year in 2007.
As of 2022, Tao had published over three hundred articles, along with sixteen books. He has an Erdős number of 2. He is a highly cited researcher.
An article by New Scientist writes of his ability:
Such is Tao's reputation that mathematicians now compete to interest him in their problems, and he is becoming a kind of Mr. Fix-it for frustrated researchers. "If you're stuck on a problem, then one way out is to interest Terence Tao," says Charles Fefferman [professor of mathematics at Princeton University].
British mathematician and Fields medalist Timothy Gowers remarked on Tao's breadth of knowledge:
Tao's mathematical knowledge has an extraordinary combination of breadth and depth: he can write confidently and authoritatively on topics as diverse as partial differential equations, analytic number theory, the geometry of 3-manifolds, nonstandard analysis, group theory, model theory, quantum mechanics, probability, ergodic theory, combinatorics, harmonic analysis, image processing, functional analysis, and many others. Some of these are areas to which he has made fundamental contributions. Others are areas that he appears to understand at the deep intuitive level of an expert despite officially not working in those areas. How he does all this, as well as writing papers and books at a prodigious rate, is a complete mystery. It has been said that David Hilbert was the last person to know all of mathematics, but it is not easy to find gaps in Tao's knowledge, and if you do then you may well find that the gaps have been filled a year later.
Research contributions
Dispersive partial differential equations
From 2001 to 2010, Tao was part of a collaboration with James Colliander, Markus Keel, Gigliola Staffilani, and Hideo Takaoka. They found a number of novel results, many to do with the well-posedness of weak solutions, for Schrödinger equations, KdV equations, and KdV-type equations.[C+03]

Michael Christ, Colliander, and Tao developed methods of Carlos Kenig, Gustavo Ponce, and Luis Vega to establish ill-posedness of certain Schrödinger and KdV equations for Sobolev data of sufficiently low exponents.[CCT03] In many cases these results were sharp enough to perfectly complement well-posedness results for sufficiently large exponents as due to Bourgain, Colliander−Keel−Staffilani−Takaoka−Tao, and others. Further such notable results for Schrödinger equations were found by Tao in collaboration with Ioan Bejenaru.[BT06]
A particularly notable result of the Colliander−Keel−Staffilani−Takaoka−Tao collaboration established the long-time existence and scattering theory of a power-law Schrödinger equation in three dimensions.[C+08] Their methods, which made use of the scale-invariance of the simple power law, were extended by Tao in collaboration with Monica Vișan and Xiaoyi Zhang to deal with nonlinearities in which the scale-invariance is broken.[TVZ07] Rowan Killip, Tao, and Vișan later made notable progress on the two-dimensional problem in radial symmetry.[KTV09]
An article by Tao in 2001 considered the wave maps equation with two-dimensional domain and spherical range.[T01a] He built upon earlier innovations of Daniel Tataru, who considered wave maps valued in Minkowski space. Tao proved the global well-posedness of solutions with sufficiently small initial data. The fundamental difficulty is that Tao considers smallness relative to the critical Sobolev norm, which typically requires sophisticated techniques. Tao later adapted some of his work on wave maps to the setting of the Benjamin–Ono equation; Alexandru Ionescu and Kenig later obtained improved results with Tao's methods.[T04a]
In 2016, Tao constructed a variant of the Navier–Stokes equations which possess solutions exhibiting irregular behavior in finite time.[T16] Due to structural similarities between Tao's system and the Navier–Stokes equations themselves, it follows that any positive resolution of the Navier–Stokes existence and smoothness problem must take into account the specific nonlinear structure of the equations. In particular, certain previously proposed resolutions of the problem could not be legitimate. Tao speculated that the Navier–Stokes equations might be able to simulate a Turing complete system, and that as a consequence it might be possible to (negatively) resolve the existence and smoothness problem using a modification of his results. However, such results remain (as of 2024) conjectural.
Compressed sensing and statistics
In collaboration with Emmanuel Candes and Justin Romberg, Tao has made notable contributions to the field of compressed sensing. In mathematical terms, most of their results identify settings in which a convex optimisation problem correctly computes the solution of an optimisation problem which seems to lack a computationally tractable structure. These problems are of the nature of finding the solution of an underdetermined linear system with the minimal possible number of nonzero entries, referred to as "sparsity". Around the same time, David Donoho considered similar problems from the alternative perspective of high-dimensional geometry.
Motivated by striking numerical experiments, Candes, Romberg, and Tao first studied the case where the matrix is given by the discrete Fourier transform.[CRT06a] Candes and Tao abstracted the problem and introduced the notion of a "restricted linear isometry," which is a matrix that is quantitatively close to an isometry when restricted to certain subspaces.[CT05] They showed that it is sufficient for either exact or optimally approximate recovery of sufficiently sparse solutions. Their proofs, which involved the theory of convex duality, were markedly simplified in collaboration with Romberg, to use only linear algebra and elementary ideas of harmonic analysis.[CRT06b] These ideas and results were later improved by Candes. Candes and Tao also considered relaxations of the sparsity condition, such as power-law decay of coefficients.[CT06] They complemented these results by drawing on a large corpus of past results in random matrix theory to show that, according to the Gaussian ensemble, a large number of matrices satisfy the restricted isometry property.[CT06]
In 2007, Candes and Tao introduced a novel statistical estimator for linear regression, which they called the "Dantzig selector." They proved a number of results on its success as an estimator and model selector, roughly in parallel to their earlier work on compressed sensing.[CT07] A number of other authors have since studied the Dantzig selector, comparing it to similar objects such as the statistical lasso introduced in the 1990s. Trevor Hastie, Robert Tibshirani, and Jerome H. Friedman conclude that it is "somewhat unsatisfactory" in a number of cases. Nonetheless, it remains of significant interest in the statistical literature.
In 2009, Candes and Benjamin Recht considered an analogous problem for recovering a matrix from knowledge of only a few of its entries and the information that the matrix is of low rank. They formulated the problem in terms of convex optimisation, studying minimisation of the nuclear norm. Candes and Tao, in 2010, developed further results and techniques for the same problem.[CT10] Improved results were later found by Recht. Similar problems and results have also been considered by a number of other authors.
Random matrices
In the 1950s, Eugene Wigner initiated the study of random matrices and their eigenvalues. Wigner studied the case of hermitian and symmetric matrices, proving a "semicircle law" for their eigenvalues. In 2010, Tao and Van Vu made a major contribution to the study of non-symmetric random matrices. They showed that if n is large and the entries of a n × n matrix A are selected randomly according to any fixed probability distribution of expectation 0 and standard deviation 1, then the eigenvalues of A will tend to be uniformly scattered across the disk of radius n1/2 around the origin; this can be made precise using the language of measure theory.[TV10] This gave a proof of the long-conjectured circular law, which had previously been proved in weaker formulations by many other authors. In Tao and Vu's formulation, the circular law becomes an immediate consequence of a "universality principle" stating that the distribution of the eigenvalues can depend only on the average and standard deviation of the given component-by-component probability distribution, thereby providing a reduction of the general circular law to a calculation for specially-chosen probability distributions.
In 2011, Tao and Vu established a "four moment theorem", which applies to random hermitian matrices whose components are independently distributed, each with average 0 and standard deviation 1, and which are exponentially unlikely to be large (as for a Gaussian distribution). If one considers two such random matrices which agree on the average value of any quadratic polynomial in the diagonal entries and on the average value of any quartic polynomial in the off-diagonal entries, then Tao and Vu show that the expected value of a large number of functions of the eigenvalues will also coincide, up to an error which is uniformly controllable by the size of the matrix and which becomes arbitrarily small as the size of the matrix increases.[TV11] Similar results were obtained around the same time by László Erdös, Horng-Tzer Yau, and Jun Yin.
Analytic number theory and arithmetic combinatorics
In 2004, Tao, together with Jean Bourgain and Nets Katz, studied the additive and multiplicative structure of subsets of finite fields of prime order.[BKT04] It is well known that there are no nontrivial subrings of such a field. Bourgain, Katz, and Tao provided a quantitative formulation of this fact, showing that for any subset of such a field, the number of sums and products of elements of the subset must be quantitatively large, as compared to the size of the field and the size of the subset itself. Improvements of their result were later given by Bourgain, Alexey Glibichuk, and Sergei Konyagin.
Tao and Ben Green proved the existence of arbitrarily long arithmetic progressions in the prime numbers; this result is generally referred to as the Green–Tao theorem, and is among Tao's most well-known results.[GT08] The source of Green and Tao's arithmetic progressions is Endre Szemerédi's 1975 theorem on existence of arithmetic progressions in certain sets of integers. Green and Tao showed that one can use a "transference principle" to extend the validity of Szemerédi's theorem to further sets of integers. The Green–Tao theorem then arises as a special case, although it is not trivial to show that the prime numbers satisfy the conditions of Green and Tao's extension of the Szemerédi theorem.
In 2010, Green and Tao gave a multilinear extension of Dirichlet's celebrated theorem on arithmetic progressions. Given a k × n matrix A and a k × 1 matrix v whose components are all integers, Green and Tao give conditions on when there exist infinitely many n × 1 matrices x such that all components of Ax + v are prime numbers.[GT10] The proof of Green and Tao was incomplete, as it was conditioned upon unproven conjectures. Those conjectures were proved in later work of Green, Tao, and Tamar Ziegler.[GTZ12]
Notable awards
Terence Tao has won numerous awards for his work. Terence Tao won the Fields Medal, the highest award of mathematics, in 2006.
- 1999 – Packard Fellowship
- 2000 – Salem Prize for:
-
- "his work in Lp harmonic analysis and on related questions in geometric measure theory and partial differential equations."
- 2002 – Bôcher Memorial Prize for:
-
- Global regularity of wave maps I. Small critical Sobolev norm in high dimensions. Internat. Math. Res. Notices (2001), no. 6, 299–328.
- Global regularity of wave maps II. Small energy in two dimensions. Comm. Math. Phys. 2244 (2001), no. 2, 443–544.
- in addition to "his remarkable series of papers, written in collaboration with J. Colliander, M. Keel, G. Staffilani, and H. Takaoka, on global regularity in optimal Sobolev spaces for KdV and other equations, as well as his many deep contributions to Strichartz and bilinear estimates."
- 2003 – Clay Research Award for:
-
- his restriction theorems in Fourier analysis, his work on wave maps, his global existence theorems for KdV-type equations, and for his solution with Allen Knutson of Horn's conjecture
- 2005 – Australian Mathematical Society Medal
- 2005 – Ostrowski Prize (with Ben Green) for:
-
- "their exceptional achievements in the area of analytic and combinatorial number theory"
- 2005 – Levi L.Conant Prize (with Allen Knutson) for:
-
- their expository article "Honeycombs and Sums of Hermitian Matrices" (Notices of the AMS. 48 (2001), 175–186.)
- 2006 – Fields Medal for:
-
- "his contributions to partial differential equations, combinatorics, harmonic analysis and additive number theory"
- 2006 – MacArthur Award
- 2006 – SASTRA Ramanujan Prize
- 2006 – Sloan Fellowship
- 2007 – Fellow of the Royal Society
- 2008 – Alan T. Waterman Award for:
-
- "his surprising and original contributions to many fields of mathematics, including number theory, differential equations, algebra, and harmonic analysis"
- 2008 – Onsager Medal for:
-
- "his combination of mathematical depth, width and volume in a manner unprecedented in contemporary mathematics". His Lars Onsager lecture was entitled "Structure and randomness in the prime numbers" at NTNU, Norway.
- 2009 – Inducted into the American Academy of Arts and Sciences
- 2010 – King Faisal International Prize
- 2010 – Nemmers Prize in Mathematics
- 2010 – Polya Prize (with Emmanuel Candès)
- 2012 – Crafoord Prize
- 2012 – Simons Investigator
- 2014 – Breakthrough Prize in Mathematics
-
- "For numerous breakthrough contributions to harmonic analysis, combinatorics, partial differential equations and analytic number theory."
- 2014 – Royal Medal
- 2015 – PROSE award in the category of "Mathematics" for:
-
- "Hilbert's Fifth Problem and Related Topics" ISBN: 978-1-4704-1564-8
- 2019 – Riemann Prize
- 2019 – The Carnegie Corporation of New York honored Tao with 2019 Great Immigrant Award.
- 2020 – Princess of Asturias Award for Technical and Scientific Research, with Emmanuel Candès, for their work on compressed sensing
- 2020 – Bolyai Prize
- 2021 – IEEE Jack S. Kilby Signal Processing Medal
- 2022 – Global Australian of the Year (Advance Global Australians; Advance.org)
- 2022 – Grande Médaille
- 2023 – Alexanderson Award (with Kaisa Matomäki, Maksym Radziwiłł, Joni Teräväinen, and Tamar Ziegler) for:
-
- Higher uniformity of bounded multiplicative functions in short intervals on average. Annals of Mathematics, Second Series (2023), 197(2): 739–857.
Major publications
Research articles
| KT98. |
| TVV98. |
| KT99. | Knutson, Allen; Tao, Terence (1999). "The honeycomb model of 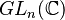 tensor products. I. Proof of the saturation conjecture". Journal of the American Mathematical Society 12 (4): 1055–1090. doi:10.1090/S0894-0347-99-00299-4. tensor products. I. Proof of the saturation conjecture". Journal of the American Mathematical Society 12 (4): 1055–1090. doi:10.1090/S0894-0347-99-00299-4. |
| C+01. |
| T01a. | (Erratum: [1]) |
| T01b. |
| C+02a. |
| C+02b. |
| MTT02. |
| CCT03. |
| C+03. | Colliander, J.; Keel, M.; Staffilani, G.; Takaoka, H.; Tao, T. (2003). "Sharp global well-posedness for KdV and modified KdV on 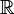 and and 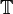 ". Journal of the American Mathematical Society 16 (3): 705–749. doi:10.1090/S0894-0347-03-00421-1. ". Journal of the American Mathematical Society 16 (3): 705–749. doi:10.1090/S0894-0347-03-00421-1. |
| T03. |
| BKT04. |
| C+04. | Colliander, J.; Keel, M.; Staffilani, G.; Takaoka, H.; Tao, T. (2004). "Global existence and scattering for rough solutions of a nonlinear Schrödinger equation on ℝ3". Communications on Pure and Applied Mathematics 57 (8): 987–1014. doi:10.1002/cpa.20029. |
| KTW04. | Knutson, Allen; Tao, Terence; Woodward, Christopher (2004). "The honeycomb model of 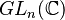 tensor products. II. Puzzles determine facets of the Littlewood–Richardson cone". Journal of the American Mathematical Society 17 (1): 19–48. doi:10.1090/S0894-0347-03-00441-7. tensor products. II. Puzzles determine facets of the Littlewood–Richardson cone". Journal of the American Mathematical Society 17 (1): 19–48. doi:10.1090/S0894-0347-03-00441-7. |
| T04a. | Tao, Terence (2004). "Global well-posedness of the Benjamin–Ono equation in H1(ℝ)". Journal of Hyperbolic Differential Equations 1 (1): 27–49. doi:10.1142/S0219891604000032. |
| T04b. |
| CT05. |
| BT06. |
| BCT06. |
| CRT06a. |
| CRT06b. |
| CT06. |
| CT07. |
| TVZ07. |
| C+08. | Colliander, J.; Keel, M.; Staffilani, G.; Takaoka, H.; Tao, T. (2008). "Global well-posedness and scattering for the energy-critical nonlinear Schrödinger equation in ℝ3". Annals of Mathematics. Second Series 167 (3): 767–865. doi:10.4007/annals.2008.167.767. |
| GT08. |
| KTV09. |
| CT10. |
| GT10. |
| TV10. |
| TV11. |
| GTZ12. |
| T16. |
See also
 In Spanish: Terence Tao para niños
In Spanish: Terence Tao para niños



