Alutor language facts for kids
Contents
By culture / time period
| Name | Base | Sample | Approx. First Appearance | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Alutor Numerals | 35,000 BCE | |||||||||||
| Babylonian numerals | 60 | 3,100 BCE | ||||||||||
| Egyptian numerals | 10 |
|
3,000 BCE | |||||||||
| Chinese numerals, Japanese numerals, Korean numerals (Sino-Korean), Vietnamese numerals (Sino-Vietnamese) | 10 |
零一二三四五六七八九十百千萬億 (Default, Traditional Chinese) 〇一二三四五六七八九十百千万亿 (Default, Simplified Chinese) 零壹貳參肆伍陸柒捌玖拾佰仟萬億 (Financial, T. Chinese) 零壹贰叁肆伍陆柒捌玖拾佰仟萬億 (Financial, S. Chinese) |
1,600 BCE | |||||||||
| Aegean numerals | 10 | 𐄇 𐄈 𐄉 𐄊 𐄋 𐄌 𐄍 𐄎 𐄏 ( 𐄐 𐄑 𐄒 𐄓 𐄔 𐄕 𐄖 𐄗 𐄘 ( 𐄙 𐄚 𐄛 𐄜 𐄝 𐄞 𐄟 𐄠 𐄡 ( 𐄢 𐄣 𐄤 𐄥 𐄦 𐄧 𐄨 𐄩 𐄪 ( 𐄫 𐄬 𐄭 𐄮 𐄯 𐄰 𐄱 𐄲 𐄳 ( |
1,500 BCE | |||||||||
| Roman numerals | I V X L C D M | 1,000 BCE | ||||||||||
| Hebrew numerals | 10 | א ב ג ד ה ו ז ח ט י כ ל מ נ ס ע פ צ ק ר ש ת ך ם ן ף ץ |
800 BCE | |||||||||
| Indian numerals | 10 | Tamil ௦ ௧ ௨ ௩ ௪ ௫ ௬ ௭ ௮ ௯
Devanagari ० १ २ ३ ४ ५ ६ ७ ८ ९ Tibetan ༠ ༡ ༢ ༣ ༤ ༥ ༦ ༧ ༨ ༩ |
750 – 690 BCE | |||||||||
| Greek numerals | 10 | ō α β γ δ ε ϝ ζ η θ ι ο Αʹ Βʹ Γʹ Δʹ Εʹ Ϛʹ Ζʹ Ηʹ Θʹ |
<400 BCE | |||||||||
| Phoenician numerals | 10 | 𐤙 𐤘 𐤗 𐤛𐤛𐤛 𐤛𐤛𐤚 𐤛𐤛𐤖 𐤛𐤛 𐤛𐤚 𐤛𐤖 𐤛 𐤚 𐤖 | <250 BCE | |||||||||
| Chinese rod numerals | 10 | 𝍠 𝍡 𝍢 𝍣 𝍤 𝍥 𝍦 𝍧 𝍨 𝍩 | 1st Century | |||||||||
| Ge'ez numerals | 10 | ፩, ፪, ፫, ፬, ፭, ፮, ፯, ፰, ፱ ፲, ፳, ፴, ፵, ፶, ፷, ፸, ፹, ፺, ፻ |
3rd – 4th Century, 15th Century (Modern Style) | |||||||||
| Armenian numerals | 10 | Ա Բ Գ Դ Ե Զ Է Ը Թ Ժ | Early 5th Century | |||||||||
| Khmer numerals | 10 | ០ ១ ២ ៣ ៤ ៥ ៦ ៧ ៨ ៩ | Early 7th Century | |||||||||
| Thai numerals | 10 | ๐ ๑ ๒ ๓ ๔ ๕ ๖ ๗ ๘ ๙ | 7th Century | |||||||||
| Abjad numerals | 10 | غ ظ ض ذ خ ث ت ش ر ق ص ف ع س ن م ل ك ي ط ح ز و هـ د ج ب ا | <8th Century | |||||||||
| Eastern Arabic numerals | 10 | ٩ ٨ ٧ ٦ ٥ ٤ ٣ ٢ ١ ٠ | 8th Century | |||||||||
| Western Arabic numerals | 10 | 0 1 2 3 4 5 6 7 8 9 | 9th Century | |||||||||
| Cyrillic numerals | 10 | А҃ В҃ Г҃ Д҃ Е҃ Ѕ҃ З҃ И҃ Ѳ҃ І҃ ... | 10th Century | |||||||||
| Tangut numerals | 10 | 𘈩𗍫𘕕𗥃𗏁𗤁𗒹𘉋𗢭𗰗 | 1036 | |||||||||
| Burmese numerals | 10 | ၀ ၁ ၂ ၃ ၄ ၅ ၆ ၇ ၈ ၉ | 11th Century | |||||||||
| Maya numerals | 20 | <15th Century | ||||||||||
| Muisca numerals | 20 | 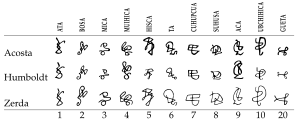 |
<15th Century | |||||||||
| Aztec numerals | 20 | 16th Century | ||||||||||
| Sinhala numerals | 10 | ෦ ෧ ෨ ෩ ෪ ෫ ෬ ෭ ෮ ෯
𑇡 𑇢 𑇣 𑇤 𑇥 𑇦 𑇧 𑇨 𑇩 𑇪 𑇫 𑇬 𑇭 𑇮 𑇯 𑇰 𑇱 𑇲 𑇳 𑇴 |
<18th Century | |||||||||
| Kaktovik Inupiaq numerals | 20 | 1994 |
By type of notation
Quick facts for kids Algerian Arabic |
||||
|---|---|---|---|---|
| Darja, دارجة | ||||
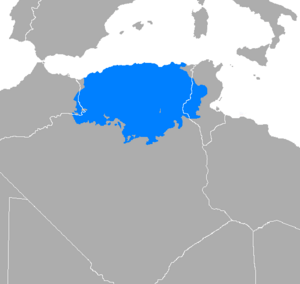
| Native to | Algeria | |||
| Native speakers | 42.5 million (2020)e18 3 million L2 speakers in Algeria (no date) |
|||
| Language family |
Afro-Asiatic
|
|||
| Writing system | Arabic script | |||
 |
||||
|
||||
Algerian Arabic (known as Darja in Algeria) is a dialect derived from the form of Arabic spoken in northern Algeria. It belongs to the Maghrebi Arabic language continuum and is partially mutually intelligible with Tunisian and Moroccan.
Like other varieties of Maghrebi Arabic, Algerian has a mostly Semitic vocabulary. It contains Berber and Latin (African Romance) influences and has numerous loanwords from French, Andalusian Arabic, Ottoman Turkish and Spanish.
Algerian Arabic is the native dialect of 75% to 80% of Algerians and is mastered by 85% to 100% of them. It is a spoken language used in daily communication and entertainment, while Modern Standard Arabic (MSA) is generally reserved for official use and education.
Standard positional numeral systems
The common names are derived somewhat arbitrarily from a mix of Latin and Greek, in some cases including roots from both languages within a single name. There have been some proposals for standardisation.
| Base | Name | Usage |
|---|---|---|
| 2 | Binary | Digital computing, imperial and customary volume (bushel-kenning-peck-gallon-pottle-quart-pint-cup-gill-jack-fluid ounce-tablespoon) |
| 3 | Ternary | Cantor set (all points in [0,1] that can be represented in ternary with no 1s); counting Tasbih in Islam; hand-foot-yard and teaspoon-tablespoon-shot measurement systems; most economical integer base |
| 4 | Quaternary | Data transmission, DNA bases and Hilbert curves; Chumashan languages, and Kharosthi numerals |
| 5 | Quinary | Gumatj, Ateso, Nunggubuyu, Kuurn Kopan Noot, and Saraveca languages; common count grouping e.g. tally marks |
| 6 | Senary | Diceware, Ndom, Kanum, and Proto-Uralic language (suspected) |
| 7 | Septenary | Weeks timekeeping, Western music letter notation |
| 8 | Octal | Charles XII of Sweden, Unix-like permissions, Squawk codes, DEC PDP-11, compact notation for binary numbers, Xiantian (I Ching, China) |
| 9 | Nonary | Base9 encoding; compact notation for ternary |
| 10 | Decimal / Denary | Most widely used by modern civilizations |
| 11 | Undecimal | Jokingly proposed during the French Revolution to settle a dispute between those proposing a shift to duodecimal and those who were content with decimal; check digit in ISBN. A base-11 number system was attributed to the Māori (New Zealand) in the 19th century and the Pangwa (Tanzania) in the 20th century. |
| 12 | Duodecimal | Languages in the Nigerian Middle Belt Janji, Gbiri-Niragu, Piti, and the Nimbia dialect of Gwandara; Chepang language of Nepal, and the Mahl dialect of Maldivian; dozen-gross-great gross counting; 12-hour clock and months timekeeping; years of Chinese zodiac; foot and inch; Roman fractions |
| 13 | Tridecimal | Base13 encoding; Conway base 13 function |
| 14 | Tetradecimal | Programming for the HP 9100A/B calculator and image processing applications; pound and stone |
| 15 | Pentadecimal | Telephony routing over IP, and the Huli language |
| 16 | Hexadecimal | Base16 encoding; compact notation for binary data; tonal system; ounce and pound |
| 17 | Heptadecimal | Base17 encoding |
| 18 | Octodecimal | Base18 encoding |
| 19 | Enneadecimal | Base19 encoding |
| 20 | Vigesimal | Basque, Celtic, Maya, Muisca, Inuit, Yoruba, Tlingit, and Dzongkha numerals; Santali, and Ainu languages |
| 21 | Unvigesimal | Base21 encoding |
| 22 | Duovigesimal | Base22 encoding |
| 23 | Trivigesimal | Kalam language, Kobon language |
| 24 | Tetravigesimal | 24-hour clock timekeeping; Kaugel language |
| 25 | Pentavigesimal | Base25 encoding |
| 26 | Hexavigesimal | Base26 encoding; sometimes used for encryption or ciphering, using all letters |
| 27 | Heptavigesimal Septemvigesimal | Telefol and Oksapmin languages. Mapping the nonzero digits to the alphabet and zero to the space is occasionally used to provide checksums for alphabetic data such as personal names, to provide a concise encoding of alphabetic strings, or as the basis for a form of gematria. Compact notation for ternary. |
| 28 | Octovigesimal | Base28 encoding; months timekeeping |
| 29 | Enneavigesimal | Base29 |
| 30 | Trigesimal | The Natural Area Code, this is the smallest base such that all of 1/2 to 1/6 terminate, a number n is a regular number if and only if 1/n terminates in base 30 |
| 31 | Untrigesimal | Base31 |
| 32 | Duotrigesimal | Base32 encoding and the Ngiti language |
| 33 | Tritrigesimal | Use of letters (except I, O, Q) with digits in vehicle registration plates of Hong Kong |
| 34 | Tetratrigesimal | Using all numbers and all letters except I and O |
| 35 | Pentatrigesimal | Using all numbers and all letters except O |
| 36 | Hexatrigesimal | Base36 encoding; use of letters with digits |
| 37 | Heptatrigesimal | Base37; using all numbers and all letters of the Spanish alphabet |
| 38 | Octotrigesimal | Base38 encoding; use all duodecimal digits and all letters |
| 40 | Quadragesimal | DEC RADIX 50/MOD40 encoding used to compactly represent file names and other symbols on Digital Equipment Corporation computers. The character set is a subset of ASCII consisting of space, upper case letters, the punctuation marks "$", ".", and "%", and the numerals. |
| 42 | Duoquadragesimal | Base42 encoding |
| 45 | Pentaquadragesimal | Base45 encoding |
| 48 | Octoquadragesimal | Base48 encoding |
| 49 | Enneaquadragesimal | Compact notation for septenary |
| 50 | Quinquagesimal | Base50 encoding; SQUOZE encoding used to compactly represent file names and other symbols on some IBM computers. Encoding using all Gurmukhi characters plus the Gurmukhi digits. |
| 52 | Duoquinquagesimal | Base52 encoding, a variant of Base62 without vowels or a variant of Base26 using all lower and upper case letters. |
| 54 | Tetraquinquagesimal | Base54 encoding |
| 56 | Hexaquinquagesimal | Base56 encoding, a variant of Base58 |
| 57 | Heptaquinquagesimal | Base57 encoding, a variant of Base62 excluding I, O, l, U, and u or I, 1, l, 0, and O |
| 58 | Octoquinquagesimal | Base58 encoding, a variant of Base62 excluding 0 (zero), I (capital i), O (capital o) and l (lower case L). |
| 60 | Sexagesimal | Babylonian numerals; NewBase60 encoding, similar to Base62, excluding I, O, and l, but including _(underscore); degrees-minutes-seconds and hours-minutes-seconds measurement systems; Ekari and Sumerian languages |
| 62 | Duosexagesimal | Base62 encoding, using 0–9, A–Z, and a–z |
| 64 | Tetrasexagesimal | Base64 encoding; I Ching in China. This system is conveniently coded into ASCII by using the 26 letters of the Latin alphabet in both upper and lower case (52 total) plus 10 numerals (62 total) and then adding two special characters (for example, YouTube video codes use the hyphen and underscore characters, - and _ to total 64). |
| 72 | Duoseptuagesimal | Base72 encoding |
| 80 | Octogesimal | Base80 encoding |
| 81 | Unoctogesimal | Base81 encoding, using as 81=34 is related to ternary |
| 85 | Pentoctogesimal | Ascii85 encoding. This is the minimum number of characters needed to encode a 32 bit number into 5 printable characters in a process similar to MIME-64 encoding, since 855 is only slightly bigger than 232. Such method is 6.7% more efficient than MIME-64 which encodes a 24 bit number into 4 printable characters. |
| 90 | Nonagesimal | Related to Goormaghtigh conjecture for the generalized repunit numbers. |
| 91 | Unnonagesimal | Base91 encoding, using all ASCII except "-" (0x2D), "\" (0x5C), and " (0x27); one variant uses "\" (0x5C) in place of """ (0x22). |
| 92 | Duononagesimal | Base92 encoding, using all of ASCII except for "`" (0x60) and """ (0x22) due to confusability. |
| 93 | Trinonagesimal | Base93 encoding, using all of ASCII printable characters except for "," (0x27) and "-" (0x3D) as well as the Space character. "," is reserved for delimiter and "-" is reserved for negation. |
| 94 | Tetranonagesimal | Base94 encoding, using all of ASCII printable characters. |
| 95 | Pentanonagesimal | Base95 encoding, a variant of Base94 with the addition of the Space character. |
| 96 | Hexanonagesimal | Base96 encoding, using all of ASCII printable characters as well as the two extra duodecimal digits |
| 100 | Centesimal | As 100=102, these are two decimal digits |
| 120 | Centevigesimal | Base120 encoding |
| 121 | Centeunvigesimal | Related to base 11 |
| 125 | Centepentavigesimal | Related to base 5 |
| 128 | Centeoctovigesimal | Using as 128=27 |
| 144 | Centetetraquadragesimal | Two duodecimal digits |
| 256 | Duocentehexaquinquagesimal | Base256 encoding, as 256=28 |
| 360 | Trecentosexagesimal | Degrees for angle |
Non-standard positional numeral systems
Bijective numeration
| Base | Name | Usage |
|---|---|---|
| 1 | Unary (Bijective base-1) | Tally marks |
| 2 | Bijective base-2 | |
| 3 | Bijective base-3 | |
| 4 | Bijective base-4 | |
| 5 | Bijective base-5 | |
| 6 | Bijective base-6 | |
| 8 | Bijective base-8 | |
| 10 | Bijective base-10 | |
| 12 | Bijective base-12 | |
| 16 | Bijective base-16 | |
| 26 | Bijective base-26 | Spreadsheet column numeration. Also used by John Nash as part of his obsession with numerology and the uncovering of "hidden" messages. |
Non-positional notation
All known numeral systems developed before the Babylonian numerals are non-positional, as are many developed later, such as the Roman numerals. The French Cistercian monks created their own numeral system.
History
Immediately after conquering Ryūkyū, Satsuma conducted a land survey in Okinawa in 1609 and in Yaeyama in 1611. By doing so, Satsuma decided the amount of tribute to be paid annually by Ryūkyū. Following that, Ryūkyū imposed a poll tax on Yaeyama in 1640. A fixed quota was allocated to each island and then was broken up into each community. Finally, quotas were set for the individual islanders, adjusted only by age and gender. Community leaders were notified of quotas in the government office on Ishigaki. They checked the calculation using warazan (barazan in Yaeyama), a straw-based method of calculation and recording numerals that was reminiscent of Incan Quipu. After that, the quota for each household was written on a wooden plate called itafuda or hansatsu (板札). That was where Kaidā glyphs were used. Although sōrō-style Written Japanese had the status of administrative language, the remote islands had to rely on pictograms to notify illiterate peasants. According to a 19th-century document cited by the Yaeyama rekishi (1954), an official named Ōhama Seiki designed "perfect ideographs" for itafuda in the early 19th century although it suggests the existence of earlier, "imperfect" ideographs. Sudō (1944) recorded an oral history on Yonaguni: 9 generations ago, an ancestor of the Kedagusuku lineage named Mase taught Kaidā glyphs and warazan to the public. Sudō dated the event to the second half of the 17th century.
According to Ikema (1959), Kaidā glyphs and warazan were evidently accurate enough to make corrections to official announcements. The poll tax was finally abolished in 1903. They were used until the introduction of the nationwide primary education system rapidly lowered the illiteracy rate during the Meiji period. They are currently used on Yonaguni and Taketomi for folk art, T-shirts, and other products, more for their artistic value than as a record-keeping system.
Non-standard positional numeral systems
Bijective numeration
| Base | Name | Usage |
|---|---|---|
| 1 | Unary (Bijective base-1) | Tally marks |
| 2 | Bijective base-2 | |
| 3 | Bijective base-3 | |
| 4 | Bijective base-4 | |
| 5 | Bijective base-5 | |
| 6 | Bijective base-6 | |
| 8 | Bijective base-8 | |
| 10 | Bijective base-10 | |
| 12 | Bijective base-12 | |
| 16 | Bijective base-16 | |
| 26 | Bijective base-26 | Spreadsheet column numeration. Also used by John Nash as part of his obsession with numerology and the uncovering of "hidden" messages. |
Negative bases
The common names of the negative base numeral systems are formed using the prefix nega-, giving names such as:
| Base | Name | Usage |
|---|---|---|
| −2 | Negabinary | |
| −3 | Negaternary | |
| −4 | Negaquaternary | |
| −5 | Negaquinary | |
| −6 | Negasenary | |
| −8 | Negaoctal | |
| −10 | Negadecimal | |
| −12 | Negaduodecimal | |
| −16 | Negahexadecimal |
By type of notation

The common names are derived somewhat arbitrarily from a mix of Latin and Greek, in some cases including roots from both languages within a single name. There have been some proposals for standardisation.
| Base | Name | Usage |
|---|---|---|
| 2 | Binary | Digital computing, imperial and customary volume (bushel-kenning-peck-gallon-pottle-quart-pint-cup-gill-jack-fluid ounce-tablespoon) |
| 3 | Ternary | Cantor set (all points in [0,1] that can be represented in ternary with no 1s); counting Tasbih in Islam; hand-foot-yard and teaspoon-tablespoon-shot measurement systems; most economical integer base |
| 4 | Quaternary | Data transmission, DNA bases and Hilbert curves; Chumashan languages, and Kharosthi numerals |
| 5 | Quinary | Gumatj, Ateso, Nunggubuyu, Kuurn Kopan Noot, and Saraveca languages; common count grouping e.g. tally marks |
| 6 | Senary | Diceware, Ndom, Kanum, and Proto-Uralic language (suspected) |
| 7 | Septenary | Weeks timekeeping, Western music letter notation |
| 8 | Octal | Charles XII of Sweden, Unix-like permissions, Squawk codes, DEC PDP-11, compact notation for binary numbers, Xiantian (I Ching, China) |
| 9 | Nonary | Base9 encoding; compact notation for ternary |
| 10 | Decimal / Denary | Most widely used by modern civilizations |
| 11 | Undecimal | Jokingly proposed during the French Revolution to settle a dispute between those proposing a shift to duodecimal and those who were content with decimal; check digit in ISBN. A base-11 number system was attributed to the Māori (New Zealand) in the 19th century and the Pangwa (Tanzania) in the 20th century. |
| 12 | Duodecimal | Languages in the Nigerian Middle Belt Janji, Gbiri-Niragu, Piti, and the Nimbia dialect of Gwandara; Chepang language of Nepal, and the Mahl dialect of Maldivian; dozen-gross-great gross counting; 12-hour clock and months timekeeping; years of Chinese zodiac; foot and inch; Roman fractions |
| 13 | Tridecimal | Base13 encoding; Conway base 13 function |
| 14 | Tetradecimal | Programming for the HP 9100A/B calculator and image processing applications; pound and stone |
| 15 | Pentadecimal | Telephony routing over IP, and the Huli language |
| 16 | Hexadecimal | Base16 encoding; compact notation for binary data; tonal system; ounce and pound |
| 17 | Heptadecimal | Base17 encoding |
| 18 | Octodecimal | Base18 encoding |
| 19 | Enneadecimal | Base19 encoding |
| 20 | Vigesimal | Basque, Celtic, Maya, Muisca, Inuit, Yoruba, Tlingit, and Dzongkha numerals; Santali, and Ainu languages |
| 21 | Unvigesimal | Base21 encoding |
| 22 | Duovigesimal | Base22 encoding |
| 23 | Trivigesimal | Kalam language, Kobon language |
| 24 | Tetravigesimal | 24-hour clock timekeeping; Kaugel language |
| 25 | Pentavigesimal | Base25 encoding |
| 26 | Hexavigesimal | Base26 encoding; sometimes used for encryption or ciphering, using all letters |
| 27 | Heptavigesimal Septemvigesimal | Telefol and Oksapmin languages. Mapping the nonzero digits to the alphabet and zero to the space is occasionally used to provide checksums for alphabetic data such as personal names, to provide a concise encoding of alphabetic strings, or as the basis for a form of gematria. Compact notation for ternary. |
| 28 | Octovigesimal | Base28 encoding; months timekeeping |
| 29 | Enneavigesimal | Base29 |
| 30 | Trigesimal | The Natural Area Code, this is the smallest base such that all of 1/2 to 1/6 terminate, a number n is a regular number if and only if 1/n terminates in base 30 |
| 31 | Untrigesimal | Base31 |
| 32 | Duotrigesimal | Base32 encoding and the Ngiti language |
| 33 | Tritrigesimal | Use of letters (except I, O, Q) with digits in vehicle registration plates of Hong Kong |
| 34 | Tetratrigesimal | Using all numbers and all letters except I and O |
| 35 | Pentatrigesimal | Using all numbers and all letters except O |
| 36 | Hexatrigesimal | Base36 encoding; use of letters with digits |
| 37 | Heptatrigesimal | Base37; using all numbers and all letters of the Spanish alphabet |
| 38 | Octotrigesimal | Base38 encoding; use all duodecimal digits and all letters |
| 40 | Quadragesimal | DEC RADIX 50/MOD40 encoding used to compactly represent file names and other symbols on Digital Equipment Corporation computers. The character set is a subset of ASCII consisting of space, upper case letters, the punctuation marks "$", ".", and "%", and the numerals. |
| 42 | Duoquadragesimal | Base42 encoding |
| 45 | Pentaquadragesimal | Base45 encoding |
| 48 | Octoquadragesimal | Base48 encoding |
| 49 | Enneaquadragesimal | Compact notation for septenary |
| 50 | Quinquagesimal | Base50 encoding; SQUOZE encoding used to compactly represent file names and other symbols on some IBM computers. Encoding using all Gurmukhi characters plus the Gurmukhi digits. |
| 52 | Duoquinquagesimal | Base52 encoding, a variant of Base62 without vowels or a variant of Base26 using all lower and upper case letters. |
| 54 | Tetraquinquagesimal | Base54 encoding |
| 56 | Hexaquinquagesimal | Base56 encoding, a variant of Base58 |
| 57 | Heptaquinquagesimal | Base57 encoding, a variant of Base62 excluding I, O, l, U, and u or I, 1, l, 0, and O |
| 58 | Octoquinquagesimal | Base58 encoding, a variant of Base62 excluding 0 (zero), I (capital i), O (capital o) and l (lower case L). |
| 60 | Sexagesimal | Babylonian numerals; NewBase60 encoding, similar to Base62, excluding I, O, and l, but including _(underscore); degrees-minutes-seconds and hours-minutes-seconds measurement systems; Ekari and Sumerian languages |
| 62 | Duosexagesimal | Base62 encoding, using 0–9, A–Z, and a–z |
| 64 | Tetrasexagesimal | Base64 encoding; I Ching in China. This system is conveniently coded into ASCII by using the 26 letters of the Latin alphabet in both upper and lower case (52 total) plus 10 numerals (62 total) and then adding two special characters (for example, YouTube video codes use the hyphen and underscore characters, - and _ to total 64). |
| 72 | Duoseptuagesimal | Base72 encoding |
| 80 | Octogesimal | Base80 encoding |
| 81 | Unoctogesimal | Base81 encoding, using as 81=34 is related to ternary |
| 85 | Pentoctogesimal | Ascii85 encoding. This is the minimum number of characters needed to encode a 32 bit number into 5 printable characters in a process similar to MIME-64 encoding, since 855 is only slightly bigger than 232. Such method is 6.7% more efficient than MIME-64 which encodes a 24 bit number into 4 printable characters. |
| 90 | Nonagesimal | Related to Goormaghtigh conjecture for the generalized repunit numbers. |
| 91 | Unnonagesimal | Base91 encoding, using all ASCII except "-" (0x2D), "\" (0x5C), and " (0x27); one variant uses "\" (0x5C) in place of """ (0x22). |
| 92 | Duononagesimal | Base92 encoding, using all of ASCII except for "`" (0x60) and """ (0x22) due to confusability. |
| 93 | Trinonagesimal | Base93 encoding, using all of ASCII printable characters except for "," (0x27) and "-" (0x3D) as well as the Space character. "," is reserved for delimiter and "-" is reserved for negation. |
| 94 | Tetranonagesimal | Base94 encoding, using all of ASCII printable characters. |
| 95 | Pentanonagesimal | Base95 encoding, a variant of Base94 with the addition of the Space character. |
| 96 | Hexanonagesimal | Base96 encoding, using all of ASCII printable characters as well as the two extra duodecimal digits |
| 100 | Centesimal | As 100=102, these are two decimal digits |
| 120 | Centevigesimal | Base120 encoding |
| 121 | Centeunvigesimal | Related to base 11 |
| 125 | Centepentavigesimal | Related to base 5 |
| 128 | Centeoctovigesimal | Using as 128=27 |
| 144 | Centetetraquadragesimal | Two duodecimal digits |
| 256 | Duocentehexaquinquagesimal | Base256 encoding, as 256=28 |
| 360 | Trecentosexagesimal | Degrees for angle |
Non-standard positional numeral systems
Bijective numeration
| Base | Name | Usage |
|---|---|---|
| 1 | Unary (Bijective base-1) | Tally marks |
| 2 | Bijective base-2 | |
| 3 | Bijective base-3 | |
| 4 | Bijective base-4 | |
| 5 | Bijective base-5 | |
| 6 | Bijective base-6 | |
| 8 | Bijective base-8 | |
| 10 | Bijective base-10 | |
| 12 | Bijective base-12 | |
| 16 | Bijective base-16 | |
| 26 | Bijective base-26 | Spreadsheet column numeration. Also used by John Nash as part of his obsession with numerology and the uncovering of "hidden" messages. |
Signed-digit representation
| Base | Name | Usage |
|---|---|---|
| 2 | Balanced binary (Non-adjacent form) | |
| 3 | Balanced ternary | Ternary computers |
| 4 | Balanced quaternary | |
| 5 | Balanced quinary | |
| 6 | Balanced senary | |
| 7 | Balanced septenary | |
| 8 | Balanced octal | |
| 9 | Balanced nonary | |
| 10 | Balanced decimal | John Colson Augustin Cauchy |
| 11 | Balanced undecimal | |
| 12 | Balanced duodecimal |
Negative bases
The common names of the negative base numeral systems are formed using the prefix nega-, giving names such as:
| Base | Name | Usage |
|---|---|---|
| −2 | Negabinary | |
| −3 | Negaternary | |
| −4 | Negaquaternary | |
| −5 | Negaquinary | |
| −6 | Negasenary | |
| −8 | Negaoctal | |
| −10 | Negadecimal | |
| −12 | Negaduodecimal | |
| −16 | Negahexadecimal |
Complex bases
| Base | Name | Usage |
|---|---|---|
| 2i | Quater-imaginary base | related to base −4 and base 16 |
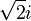 |
Base 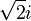 |
related to base −2 and base 4 |
![\sqrt[4]{2}i](/images/math/d/c/d/dcddbe42b530a2387636f0d5f283ceb6.png) |
Base ![\sqrt[4]{2}i](/images/math/d/c/d/dcddbe42b530a2387636f0d5f283ceb6.png) |
related to base 2 |
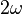 |
Base 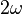 |
related to base 8 |
![\sqrt[3]{2} \omega](/images/math/8/e/2/8e246ae181c3a3053e63bfd7a6b0789b.png) |
Base ![\sqrt[3]{2} \omega](/images/math/8/e/2/8e246ae181c3a3053e63bfd7a6b0789b.png) |
related to base 2 |
| −1 ± i | Twindragon base | Twindragon fractal shape, related to base −4 and base 16 |
| 1 ± i | Nega-Twindragon base | related to base −4 and base 16 |
Non-integer bases
| Base | Name | Usage |
|---|---|---|
 |
Base  |
a rational non-integer base |
 |
Base  |
related to duodecimal |
 |
Base  |
related to decimal |
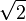 |
Base 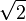 |
related to base 2 |
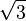 |
Base 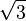 |
related to base 3 |
![\sqrt[3]{2}](/images/math/6/2/f/62f6a0ce6cf44d89c6f3b211c98c43bd.png) |
Base ![\sqrt[3]{2}](/images/math/6/2/f/62f6a0ce6cf44d89c6f3b211c98c43bd.png) |
|
![\sqrt[4]{2}](/images/math/b/b/e/bbed5c0cb24e50ec62fc424f7b80f157.png) |
Base ![\sqrt[4]{2}](/images/math/b/b/e/bbed5c0cb24e50ec62fc424f7b80f157.png) |
|
![\sqrt[12]{2}](/images/math/7/0/b/70b8b8fc763c20423a65bd934e378085.png) |
Base ![\sqrt[12]{2}](/images/math/7/0/b/70b8b8fc763c20423a65bd934e378085.png) |
using in music scale |
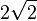 |
Base 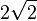 |
|
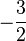 |
Base 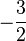 |
a negative rational non-integer base |
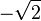 |
Base 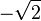 |
a negative non-integer base, related to base 2 |
 |
Base  |
related to decimal |
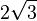 |
Base 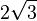 |
related to duodecimal |
| φ | Golden ratio base | Early Beta encoder |
| ρ | Plastic number base | |
| ψ | Supergolden ratio base | |
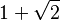 |
Silver ratio base | |
| e | Base  |
Lowest radix economy |
| π | Base 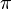 |
|
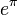 |
Base 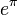 |
n-adic number
| Base | Name | Usage |
|---|---|---|
| 2 | Dyadic number | |
| 3 | Triadic number | |
| 4 | Tetradic number | the same as dyadic number |
| 5 | Pentadic number | |
| 6 | Hexadic number | not a field |
| 7 | Heptadic number | |
| 8 | Octadic number | the same as dyadic number |
| 9 | Enneadic number | the same as triadic number |
| 10 | Decadic number | not a field |
| 11 | Hendecadic number | |
| 12 | Dodecadic number | not a field |
Mixed radix
- Factorial number system {1, 2, 3, 4, 5, 6, ...}
- Even double factorial number system {2, 4, 6, 8, 10, 12, ...}
- Odd double factorial number system {1, 3, 5, 7, 9, 11, ...}
- Primorial number system {2, 3, 5, 7, 11, 13, ...}
- {60, 60, 24, 7} in timekeeping
- {60, 60, 24, 30 (or 31 or 28 or 29), 12} in timekeeping
- (12, 20) traditional English monetary system (£sd)
- (20, 18, 13) Maya timekeeping
Other
- Quote notation
- Redundant binary representation
- Hereditary base-n notation
- Asymmetric numeral systems optimized for non-uniform probability distribution of symbols
Non-positional notation
All known numeral systems developed before the Babylonian numerals are non-positional, as are many developed later, such as the Roman numerals. The French Cistercian monks created their own numeral system.
By type of notation

The common names are derived somewhat arbitrarily from a mix of Latin and Greek, in some cases including roots from both languages within a single name. There have been some proposals for standardisation.
| Base | Name | Usage |
|---|---|---|
| 2 | Binary | Digital computing, imperial and customary volume (bushel-kenning-peck-gallon-pottle-quart-pint-cup-gill-jack-fluid ounce-tablespoon) |
| 3 | Ternary | Cantor set (all points in [0,1] that can be represented in ternary with no 1s); counting Tasbih in Islam; hand-foot-yard and teaspoon-tablespoon-shot measurement systems; most economical integer base |
| 4 | Quaternary | Data transmission, DNA bases and Hilbert curves; Chumashan languages, and Kharosthi numerals |
| 5 | Quinary | Gumatj, Ateso, Nunggubuyu, Kuurn Kopan Noot, and Saraveca languages; common count grouping e.g. tally marks |
| 6 | Senary | Diceware, Ndom, Kanum, and Proto-Uralic language (suspected) |
| 7 | Septenary | Weeks timekeeping, Western music letter notation |
| 8 | Octal | Charles XII of Sweden, Unix-like permissions, Squawk codes, DEC PDP-11, compact notation for binary numbers, Xiantian (I Ching, China) |
| 9 | Nonary | Base9 encoding; compact notation for ternary |
| 10 | Decimal / Denary | Most widely used by modern civilizations |
| 11 | Undecimal | Jokingly proposed during the French Revolution to settle a dispute between those proposing a shift to duodecimal and those who were content with decimal; check digit in ISBN. A base-11 number system was attributed to the Māori (New Zealand) in the 19th century and the Pangwa (Tanzania) in the 20th century. |
| 12 | Duodecimal | Languages in the Nigerian Middle Belt Janji, Gbiri-Niragu, Piti, and the Nimbia dialect of Gwandara; Chepang language of Nepal, and the Mahl dialect of Maldivian; dozen-gross-great gross counting; 12-hour clock and months timekeeping; years of Chinese zodiac; foot and inch; Roman fractions |
| 13 | Tridecimal | Base13 encoding; Conway base 13 function |
| 14 | Tetradecimal | Programming for the HP 9100A/B calculator and image processing applications; pound and stone |
| 15 | Pentadecimal | Telephony routing over IP, and the Huli language |
| 16 | Hexadecimal | Base16 encoding; compact notation for binary data; tonal system; ounce and pound |
| 17 | Heptadecimal | Base17 encoding |
| 18 | Octodecimal | Base18 encoding |
| 19 | Enneadecimal | Base19 encoding |
| 20 | Vigesimal | Basque, Celtic, Maya, Muisca, Inuit, Yoruba, Tlingit, and Dzongkha numerals; Santali, and Ainu languages |
| 21 | Unvigesimal | Base21 encoding |
| 22 | Duovigesimal | Base22 encoding |
| 23 | Trivigesimal | Kalam language, Kobon language |
| 24 | Tetravigesimal | 24-hour clock timekeeping; Kaugel language |
| 25 | Pentavigesimal | Base25 encoding |
| 26 | Hexavigesimal | Base26 encoding; sometimes used for encryption or ciphering, using all letters |
| 27 | Heptavigesimal Septemvigesimal | Telefol and Oksapmin languages. Mapping the nonzero digits to the alphabet and zero to the space is occasionally used to provide checksums for alphabetic data such as personal names, to provide a concise encoding of alphabetic strings, or as the basis for a form of gematria. Compact notation for ternary. |
| 28 | Octovigesimal | Base28 encoding; months timekeeping |
| 29 | Enneavigesimal | Base29 |
| 30 | Trigesimal | The Natural Area Code, this is the smallest base such that all of 1/2 to 1/6 terminate, a number n is a regular number if and only if 1/n terminates in base 30 |
| 31 | Untrigesimal | Base31 |
| 32 | Duotrigesimal | Base32 encoding and the Ngiti language |
| 33 | Tritrigesimal | Use of letters (except I, O, Q) with digits in vehicle registration plates of Hong Kong |
| 34 | Tetratrigesimal | Using all numbers and all letters except I and O |
| 35 | Pentatrigesimal | Using all numbers and all letters except O |
| 36 | Hexatrigesimal | Base36 encoding; use of letters with digits |
| 37 | Heptatrigesimal | Base37; using all numbers and all letters of the Spanish alphabet |
| 38 | Octotrigesimal | Base38 encoding; use all duodecimal digits and all letters |
| 40 | Quadragesimal | DEC RADIX 50/MOD40 encoding used to compactly represent file names and other symbols on Digital Equipment Corporation computers. The character set is a subset of ASCII consisting of space, upper case letters, the punctuation marks "$", ".", and "%", and the numerals. |
| 42 | Duoquadragesimal | Base42 encoding |
| 45 | Pentaquadragesimal | Base45 encoding |
| 48 | Octoquadragesimal | Base48 encoding |
| 49 | Enneaquadragesimal | Compact notation for septenary |
| 50 | Quinquagesimal | Base50 encoding; SQUOZE encoding used to compactly represent file names and other symbols on some IBM computers. Encoding using all Gurmukhi characters plus the Gurmukhi digits. |
| 52 | Duoquinquagesimal | Base52 encoding, a variant of Base62 without vowels or a variant of Base26 using all lower and upper case letters. |
| 54 | Tetraquinquagesimal | Base54 encoding |
| 56 | Hexaquinquagesimal | Base56 encoding, a variant of Base58 |
| 57 | Heptaquinquagesimal | Base57 encoding, a variant of Base62 excluding I, O, l, U, and u or I, 1, l, 0, and O |
| 58 | Octoquinquagesimal | Base58 encoding, a variant of Base62 excluding 0 (zero), I (capital i), O (capital o) and l (lower case L). |
| 60 | Sexagesimal | Babylonian numerals; NewBase60 encoding, similar to Base62, excluding I, O, and l, but including _(underscore); degrees-minutes-seconds and hours-minutes-seconds measurement systems; Ekari and Sumerian languages |
| 62 | Duosexagesimal | Base62 encoding, using 0–9, A–Z, and a–z |
| 64 | Tetrasexagesimal | Base64 encoding; I Ching in China. This system is conveniently coded into ASCII by using the 26 letters of the Latin alphabet in both upper and lower case (52 total) plus 10 numerals (62 total) and then adding two special characters (for example, YouTube video codes use the hyphen and underscore characters, - and _ to total 64). |
| 72 | Duoseptuagesimal | Base72 encoding |
| 80 | Octogesimal | Base80 encoding |
| 81 | Unoctogesimal | Base81 encoding, using as 81=34 is related to ternary |
| 85 | Pentoctogesimal | Ascii85 encoding. This is the minimum number of characters needed to encode a 32 bit number into 5 printable characters in a process similar to MIME-64 encoding, since 855 is only slightly bigger than 232. Such method is 6.7% more efficient than MIME-64 which encodes a 24 bit number into 4 printable characters. |
| 90 | Nonagesimal | Related to Goormaghtigh conjecture for the generalized repunit numbers. |
| 91 | Unnonagesimal | Base91 encoding, using all ASCII except "-" (0x2D), "\" (0x5C), and " (0x27); one variant uses "\" (0x5C) in place of """ (0x22). |
| 92 | Duononagesimal | Base92 encoding, using all of ASCII except for "`" (0x60) and """ (0x22) due to confusability. |
| 93 | Trinonagesimal | Base93 encoding, using all of ASCII printable characters except for "," (0x27) and "-" (0x3D) as well as the Space character. "," is reserved for delimiter and "-" is reserved for negation. |
| 94 | Tetranonagesimal | Base94 encoding, using all of ASCII printable characters. |
| 95 | Pentanonagesimal | Base95 encoding, a variant of Base94 with the addition of the Space character. |
| 96 | Hexanonagesimal | Base96 encoding, using all of ASCII printable characters as well as the two extra duodecimal digits |
| 100 | Centesimal | As 100=102, these are two decimal digits |
| 120 | Centevigesimal | Base120 encoding |
| 121 | Centeunvigesimal | Related to base 11 |
| 125 | Centepentavigesimal | Related to base 5 |
| 128 | Centeoctovigesimal | Using as 128=27 |
| 144 | Centetetraquadragesimal | Two duodecimal digits |
| 256 | Duocentehexaquinquagesimal | Base256 encoding, as 256=28 |
| 360 | Trecentosexagesimal | Degrees for angle |
Non-standard positional numeral systems
Bijective numeration
| Base | Name | Usage |
|---|---|---|
| 1 | Unary (Bijective base-1) | Tally marks |
| 2 | Bijective base-2 | |
| 3 | Bijective base-3 | |
| 4 | Bijective base-4 | |
| 5 | Bijective base-5 | |
| 6 | Bijective base-6 | |
| 8 | Bijective base-8 | |
| 10 | Bijective base-10 | |
| 12 | Bijective base-12 | |
| 16 | Bijective base-16 |
Other
- Quote notation
- Redundant binary representation
- Hereditary base-n notation
- Asymmetric numeral systems optimized for non-uniform probability distribution of symbols
Non-positional notation
All known numeral systems developed before the Babylonian numerals are non-positional, as are many developed later, such as the Roman numerals. The French Cistercian monks created their own numeral system.
Other
- Quote notation
- Redundant binary representation
- Hereditary base-n notation
- Asymmetric numeral systems optimized for non-uniform probability distribution of symbols
Other
- Quote notation
- Redundant binary representation
- Hereditary base-n notation
- Asymmetric numeral systems optimized for non-uniform probability distribution of symbols
Other
- Quote notation
- Redundant binary representation
- Hereditary base-n notation
- Asymmetric numeral systems optimized for non-uniform probability distribution of symbols
Other
- Quote notation
- Redundant binary representation
- Hereditary base-n notation
- Asymmetric numeral systems optimized for non-uniform probability distribution of symbols
Letters
Adlam has both major and minor cases. See Omniglot in the external links for the pronunciation of the basic letters
| Capital | Minuscule | Latin | Letter Name | IPA |
|---|---|---|---|---|
| 𞤀 | 𞤢 | a | alif | a |
| 𞤁 | 𞤣 | d | dâli | d |
| 𞤂 | 𞤤 | l | lam | l |
| 𞤃 | 𞤥 | m | mim | m |
| 𞤄 | 𞤦 | b | ba | b |
| 𞤅 | 𞤧 | s | singniyhé | s |
| 𞤆 | 𞤨 | p | pè | p |
| 𞤇 | 𞤩 | ɓ (bh) | bhè | ɓ |
| 𞤈 | 𞤪 | r | ra | r/ɾ |
| 𞤉 | 𞤫 | e | è | e |
| 𞤊 | 𞤬 | f | fa | f |
| 𞤋 | 𞤭 | i | i | i |
| 𞤌 | 𞤮 | o | ö | o |
| 𞤍 | 𞤯 | ɗ (dh) | dha | ɗ |
| 𞤎 | 𞤰 | ƴ (yh) | yhè | ʔʲ |
| 𞤏 | 𞤱 | w | wâwou | w |
| 𞤐 | 𞤲 | n, any syllable-final nasal | noûn | n |
| 𞤑 | 𞤳 | k | kaf | k |
| 𞤒 | 𞤴 | y | ya | j |
| 𞤓 | 𞤵 | u | ou | u |
| 𞤔 | 𞤶 | j | djim | dʒ |
| 𞤕 | 𞤷 | c | tchi | tʃ |
| 𞤖 | 𞤸 | h | ha | h |
| 𞤗 | 𞤹 | ɠ (q) | ghaf | q |
| 𞤘 | 𞤺 | g | ga | ɡ |
| 𞤙 | 𞤻 | ñ (ny) | gna | ɲ |
| 𞤚 | 𞤼 | t | tou | t |
| 𞤛 | 𞤽 | ŋ (nh) | nha | ŋ |
| Supplemental: for other languages or for loanwords | ||||
| 𞤜 | 𞤾 | v | va | v |
| 𞤝 | 𞤿 | x (kh) | kha | x |
| 𞤞 | 𞥀 | ɡb | gbe | ɡ͡b |
| 𞤟 | 𞥁 | z | zal | z |
| 𞤠 | 𞥂 | kp | kpo | k͡p |
| 𞤡 | 𞥃 | sh | sha | ʃ |
The letters are found either joined akin to Arabic or separately - the joined form is commonly used in a cursive manner, however separate or block forms are also used as primarily for educational content.
Digits
Unlike in Arabic script, Adlam digits go in the same direction (right to left) as letters.
| Adlam | Hindu-Arabic |
|---|---|
| 𞥐 | 0 |
| 𞥑 | 1 |
| 𞥒 | 2 |
| 𞥓 | 3 |
| 𞥔 | 4 |
| 𞥕 | 5 |
| 𞥖 | 6 |
| 𞥗 | 7 |
| 𞥘 | 8 |
| 𞥙 | 9 |

