4-polytope facts for kids

Kids Encyclopedia Facts

Graphs of the six convex regular 4-polytopes
{3,3,3}	{3,3,4}	{4,3,3}
5-cell Pentatope 4-simplex	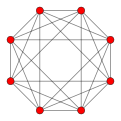16-cell Orthoplex 4-orthoplex	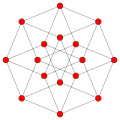8-cell Tesseract 4-cube
{3,4,3}	{3,3,5}	{5,3,3}
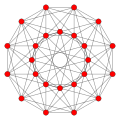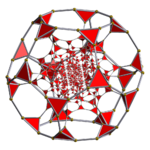
24-cell Octaplex	600-cell Tetraplex	120-cell Dodecaplex

In geometry, a 4-polytope (sometimes also called a polychoron, polycell, or polyhedroid) is a four-dimensional polytope. It is a connected and closed figure, composed of lower-dimensional polytopal elements: vertices, edges, faces (polygons), and cells (polyhedra). Each face is shared by exactly two cells. The 4-polytopes were discovered by the Swiss mathematician Ludwig Schläfli before 1853.

The two-dimensional analogue of a 4-polytope is a polygon, and the three-dimensional analogue is a polyhedron.

Topologically 4-polytopes are closely related to the uniform honeycombs, such as the cubic honeycomb, which tessellate 3-space; similarly the 3D cube is related to the infinite 2D square tiling. Convex 4-polytopes can be cut and unfolded as nets in 3-space.

Definition
Geometry
Visualisation
Topological characteristics
Classification
- Criteria
- Classes
See also

Definition

A 4-polytope is a closed four-dimensional figure. It comprises vertices (corner points), edges, faces and cells. A cell is the three-dimensional analogue of a face, and is therefore a polyhedron. Each face must join exactly two cells, analogous to the way in which each edge of a polyhedron joins just two faces. Like any polytope, the elements of a 4-polytope cannot be subdivided into two or more sets which are also 4-polytopes, i.e. it is not a compound.

Geometry

The convex regular 4-polytopes are the four-dimensional analogues of the Platonic solids. The most familiar 4-polytope is the tesseract or hypercube, the 4D analogue of the cube.

The convex regular 4-polytopes can be ordered by size as a measure of 4-dimensional content (hypervolume) for the same radius. Each greater polytope in the sequence is rounder than its predecessor, enclosing more content within the same radius. The 4-simplex (5-cell) is the limit smallest case, and the 120-cell is the largest. Complexity (as measured by comparing configuration matrices or simply the number of vertices) follows the same ordering.

Regular convex 4-polytopes
Symmetry group	A₄	B₄		F₄	H₄
Name	5-cell Hyper-tetrahedron 5-point	16-cell Hyper-octahedron 8-point	8-cell Hyper-cube 16-point	24-cell 24-point	600-cell Hyper-icosahedron 120-point	120-cell Hyper-dodecahedron 600-point
Schläfli symbol	{3, 3, 3}	{3, 3, 4}	{4, 3, 3}	{3, 4, 3}	{3, 3, 5}	{5, 3, 3}
Coxeter mirrors
Mirror dihedrals	𝝅/3 𝝅/3 𝝅/3 𝝅/2 𝝅/2 𝝅/2	𝝅/3 𝝅/3 𝝅/4 𝝅/2 𝝅/2 𝝅/2	𝝅/4 𝝅/3 𝝅/3 𝝅/2 𝝅/2 𝝅/2	𝝅/3 𝝅/4 𝝅/3 𝝅/2 𝝅/2 𝝅/2	𝝅/3 𝝅/3 𝝅/5 𝝅/2 𝝅/2 𝝅/2	𝝅/5 𝝅/3 𝝅/3 𝝅/2 𝝅/2 𝝅/2
Graph
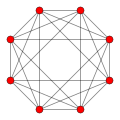Vertices	5 tetrahedral	8 octahedral	16 tetrahedral	24 cubical	120 icosahedral	600 tetrahedral
Edges	10 triangular	24 square	32 triangular	96 triangular	720 pentagonal	1200 triangular
Faces	10 triangles	32 triangles	24 squares	96 triangles	1200 triangles	720 pentagons
Cells	5 tetrahedra	16 tetrahedra	8 cubes	24 octahedra	600 tetrahedra	120 dodecahedra
Tori	1 5-tetrahedron	2 8-tetrahedron	2 4-cube	4 6-octahedron	20 30-tetrahedron	12 10-dodecahedron
Inscribed	120 in 120-cell	675 in 120-cell	2 16-cells	3 8-cells	25 24-cells	10 600-cells
Great polygons		2 squares x 3	4 rectangles x 4	4 hexagons x 4	12 decagons x 6	100 irregular hexagons x 4
Petrie polygons	1 pentagon	1 octagon	2 octagons	2 dodecagons	4 30-gons	20 30-gons
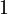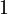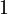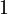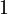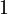Long radius	$1$	$1$	$1$	$1$	$1$	$1$
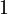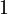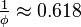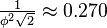Edge length	$\sqrt{\tfrac{5}{2}} \approx 1.581$	$\sqrt{2} \approx 1.414$	$1$	$1$	$\tfrac{1}{\phi} \approx 0.618$	$\tfrac{1}{\phi^2\sqrt{2}} \approx 0.270$
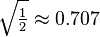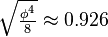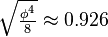Short radius	$\tfrac{1}{4}$	$\tfrac{1}{2}$	$\tfrac{1}{2}$	$\sqrt{\tfrac{1}{2}} \approx 0.707$	$\sqrt{\tfrac{\phi^4}{8}} \approx 0.926$	$\sqrt{\tfrac{\phi^4}{8}} \approx 0.926$
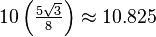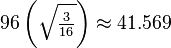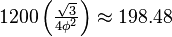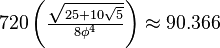Area	$10\left(\tfrac{5\sqrt{3}}{8}\right) \approx 10.825$	$32\left(\sqrt{\tfrac{3}{4}}\right) \approx 27.713$	$24$	$96\left(\sqrt{\tfrac{3}{16}}\right) \approx 41.569$	$1200\left(\tfrac{\sqrt{3}}{4\phi^2}\right) \approx 198.48$	$720\left(\tfrac{\sqrt{25+10\sqrt{5}}}{8\phi^4}\right) \approx 90.366$
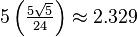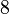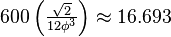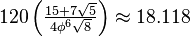Volume	$5\left(\tfrac{5\sqrt{5}}{24}\right) \approx 2.329$	$16\left(\tfrac{1}{3}\right) \approx 5.333$	$8$	$24\left(\tfrac{\sqrt{2}}{3}\right) \approx 11.314$	$600\left(\tfrac{\sqrt{2}}{12\phi^3}\right) \approx 16.693$	$120\left(\tfrac{15 + 7\sqrt{5}}{4\phi^6\sqrt{8}}\right) \approx 18.118$
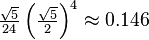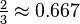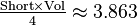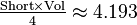4-Content	$\tfrac{\sqrt{5}}{24}\left(\tfrac{\sqrt{5}}{2}\right)^4 \approx 0.146$	$\tfrac{2}{3} \approx 0.667$	$1$	$2$	$\tfrac{\text{Short}\times\text{Vol}}{4} \approx 3.863$	$\tfrac{\text{Short}\times\text{Vol}}{4} \approx 4.193$

Visualisation

Example presentations of a 24-cell
Sectioning		Net

Projections
Schlegel	2D orthogonal	3D orthogonal

4-polytopes cannot be seen in three-dimensional space due to their extra dimension. Several techniques are used to help visualise them.

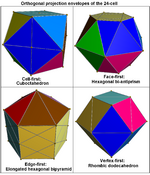
Orthogonal projection

Orthogonal projections can be used to show various symmetry orientations of a 4-polytope. They can be drawn in 2D as vertex-edge graphs, and can be shown in 3D with solid faces as visible projective envelopes.

Perspective projection

Just as a 3D shape can be projected onto a flat sheet, so a 4-D shape can be projected onto 3-space or even onto a flat sheet. One common projection is a Schlegel diagram which uses stereographic projection of points on the surface of a 3-sphere into three dimensions, connected by straight edges, faces, and cells drawn in 3-space.

Sectioning

Just as a slice through a polyhedron reveals a cut surface, so a slice through a 4-polytope reveals a cut "hypersurface" in three dimensions. A sequence of such sections can be used to build up an understanding of the overall shape. The extra dimension can be equated with time to produce a smooth animation of these cross sections.

Nets

A net of a 4-polytope is composed of polyhedral cells that are connected by their faces and all occupy the same three-dimensional space, just as the polygon faces of a net of a polyhedron are connected by their edges and all occupy the same plane.

Topological characteristics

The tesseract as a Schlegel diagram

The topology of any given 4-polytope is defined by its Betti numbers and torsion coefficients.

The value of the Euler characteristic used to characterise polyhedra does not generalize usefully to higher dimensions, and is zero for all 4-polytopes, whatever their underlying topology. This inadequacy of the Euler characteristic to reliably distinguish between different topologies in higher dimensions led to the discovery of the more sophisticated Betti numbers.

Similarly, the notion of orientability of a polyhedron is insufficient to characterise the surface twistings of toroidal 4-polytopes, and this led to the use of torsion coefficients.

Classification

Criteria

Like all polytopes, 4-polytopes may be classified based on properties like "convexity" and "symmetry".

A 4-polytope is convex if its boundary (including its cells, faces and edges) does not intersect itself and the line segment joining any two points of the 4-polytope is contained in the 4-polytope or its interior; otherwise, it is non-convex. Self-intersecting 4-polytopes are also known as star 4-polytopes, from analogy with the star-like shapes of the non-convex star polygons and Kepler–Poinsot polyhedra.
A 4-polytope is regular if it is transitive on its flags. This means that its cells are all congruent regular polyhedra, and similarly its vertex figures are congruent and of another kind of regular polyhedron.
A convex 4-polytope is semi-regular if it has a symmetry group under which all vertices are equivalent (vertex-transitive) and its cells are regular polyhedra. The cells may be of two or more kinds, provided that they have the same kind of face. There are only 3 cases identified by Thorold Gosset in 1900: the rectified 5-cell, rectified 600-cell, and snub 24-cell.
A 4-polytope is uniform if it has a symmetry group under which all vertices are equivalent, and its cells are uniform polyhedra. The faces of a uniform 4-polytope must be regular.
A 4-polytope is scaliform if it is vertex-transitive, and has all equal length edges. This allows cells which are not uniform, such as the regular-faced convex Johnson solids.
A regular 4-polytope which is also convex is said to be a convex regular 4-polytope.
A 4-polytope is prismatic if it is the Cartesian product of two or more lower-dimensional polytopes. A prismatic 4-polytope is uniform if its factors are uniform. The hypercube is prismatic (product of two squares, or of a cube and line segment), but is considered separately because it has symmetries other than those inherited from its factors.
A tiling or honeycomb of 3-space is the division of three-dimensional Euclidean space into a repetitive grid of polyhedral cells. Such tilings or tessellations are infinite and do not bound a "4D" volume, and are examples of infinite 4-polytopes. A uniform tiling of 3-space is one whose vertices are congruent and related by a space group and whose cells are uniform polyhedra.

Classes

The following lists the various categories of 4-polytopes classified according to the criteria above:

The truncated 120-cell is one of 47 convex non-prismatic uniform 4-polytopes

Uniform 4-polytope (vertex-transitive):

Convex uniform 4-polytopes (64, plus two infinite families)
- 47 non-prismatic convex uniform 4-polytope including:
  - 6 Convex regular 4-polytope
- Prismatic uniform 4-polytopes:
  - {} × {p,q} : 18 polyhedral hyperprisms (including cubic hyperprism, the regular hypercube)
  - Prisms built on antiprisms (infinite family)
  - {p} × {q} : duoprisms (infinite family)
Non-convex uniform 4-polytopes (10 + unknown)

The great grand stellated 120-cell is the largest of 10 regular star 4-polytopes, having 600 vertices.
- 10 (regular) Schläfli-Hess polytopes
- 57 hyperprisms built on nonconvex uniform polyhedra
- Unknown total number of nonconvex uniform 4-polytopes: Norman Johnson and other collaborators have identified 2189 known cases (convex and star, excluding the infinite families), all constructed by vertex figures by Stella4D software.

Other convex 4-polytopes:

Polyhedral pyramid
Polyhedral bipyramid
Polyhedral prism

The regular cubic honeycomb is the only infinite regular 4-polytope in Euclidean 3-dimensional space.

Infinite uniform 4-polytopes of Euclidean 3-space (uniform tessellations of convex uniform cells)

28 convex uniform honeycombs: uniform convex polyhedral tessellations, including:
- 1 regular tessellation, cubic honeycomb: {4,3,4}

Infinite uniform 4-polytopes of hyperbolic 3-space (uniform tessellations of convex uniform cells)

76 Wythoffian convex uniform honeycombs in hyperbolic space, including:
- 4 regular tessellation of compact hyperbolic 3-space: {3,5,3}, {4,3,5}, {5,3,4}, {5,3,5}

Dual uniform 4-polytope (cell-transitive):

41 unique dual convex uniform 4-polytopes
17 unique dual convex uniform polyhedral prisms
infinite family of dual convex uniform duoprisms (irregular tetrahedral cells)
27 unique convex dual uniform honeycombs, including:
- Rhombic dodecahedral honeycomb
- Disphenoid tetrahedral honeycomb

Others:

Weaire–Phelan structure periodic space-filling honeycomb with irregular cells

The 11-cell is an abstract regular 4-polytope, existing in the real projective plane, it can be seen by presenting its 11 hemi-icosahedral vertices and cells by index and color.

Abstract regular 4-polytopes:

11-cell
57-cell

These categories include only the 4-polytopes that exhibit a high degree of symmetry. Many other 4-polytopes are possible, but they have not been studied as extensively as the ones included in these categories.