Stereographic projection facts for kids

Illustration by Rubens for "Opticorum libri sex philosophis juxta ac mathematicis utiles", by François d'Aiguillon. It demonstrates how the projection is computed.

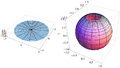
In geometry, a stereographic projection is a function that maps the points of a sphere onto a plane. The projection is defined on the entire sphere, except for one point, called the projection point.

Intuitively, the stereographic projection is a way of picturing a sphere as a plane, with some inevitable compromises. Because the sphere and the plane appear in many areas of mathematics and its applications, so does the stereographic projection; it finds use in diverse fields including complex analysis, cartography, geology, and photography. In practice, the projection is carried out by computer or by hand using a special kind of graph paper called a stereonet or Wulff net.

A simple example of such a projection, encountered in everyday life is the sun casting a shadow of a globe onto the ground.

Images for kids

• 

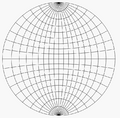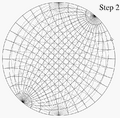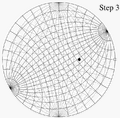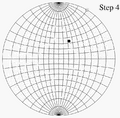
  An extension of the Wulff net, showing how meridians and parallels extend beyond the hemisphere

• 

  Stereographic projection of the world north of 30°S. 15° graticule.

• 

  Rumold Mercator's map

• 

  Joan Blaeu's map

• 

  Stereographic projection of the spherical panorama of the Last Supper sculpture by Michele Vedani in Esino Lario, Lombardy, Italy during Wikimania 2016

• 

  A Cartesian grid on the plane appears distorted on the sphere. The grid lines are still perpendicular, but the areas of the grid squares shrink as they approach the north pole.

• 

  A polar grid on the plane appears distorted on the sphere. The grid curves are still perpendicular, but the areas of the grid sectors shrink as they approach the north pole.

• 

  The sphere, with various loxodromes shown in distinct colors

• 

  Illustration of steps 1–4 for plotting a point on a Wulff net

• 

  Animation of Kikuchi lines of four of the eight zones in an fcc crystal. Planes edge-on (banded lines) intersect at fixed angles.

• 

  The rational points on a circle correspond, under stereographic projection, to the rational points of the line.

• 

  Stereographic projection is used to map the Earth, especially near the poles, but also near other points of interest.

• 

  A crystallographic pole figure for the diamond lattice in [111] direction

• 

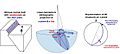
  Use of lower hemisphere stereographic projection to plot planar and linear data in structural geology, using the example of a fault plane with a slickenside lineation

See also

In Spanish: Proyección estereográfica para niños