Four-dimensional space facts for kids
A four-dimensional space (4D) is a mathematical extension of the concept of three-dimensional space (3D). Three-dimensional space is the simplest possible abstraction of the observation that one only needs three numbers, called dimensions, to describe the sizes or locations of objects in the everyday world. For example, the volume of a rectangular box is found by measuring and multiplying its length, width, and height (often labeled x, y, and z).
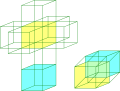
The idea of adding a fourth dimension began with Jean le Rond d'Alembert's "Dimensions" being published in 1754, was followed by Joseph-Louis Lagrange in the mid-1700s, and culminated in a precise formalization of the concept in 1854 by Bernhard Riemann. In 1880, Charles Howard Hinton popularized these insights in an essay titled "What is the Fourth Dimension?", which explained the concept of a "four-dimensional cube" with a step-by-step generalization of the properties of lines, squares, and cubes. The simplest form of Hinton's method is to draw two ordinary 3D cubes in 2D space, one encompassing the other, separated by an "unseen" distance, and then draw lines between their equivalent vertices. This can be seen in the accompanying animation whenever it shows a smaller inner cube inside a larger outer cube. The eight lines connecting the vertices of the two cubes in this case represent a single direction in the "unseen" fourth dimension.
Higher-dimensional spaces (i.e., greater than three) have since become one of the foundations for formally expressing modern mathematics and physics. Large parts of these topics could not exist in their current forms without using such spaces. Einstein's concept of spacetime uses such a 4D space, though it has a Minkowski structure that is slightly more complicated than Euclidean 4D space.
Four-dimensional perception in humans
Research using virtual reality finds that humans, despite living in a three-dimensional world, can, without special practice, make spatial judgments about line segments embedded in four-dimensional space. In another study, the ability of humans to orient themselves in 2D, 3D, and 4D mazes has been tested. Each maze consisted of four path segments of random length and connected with orthogonal random bends, but without branches or loops (i.e. actually labyrinths). The graphical interface was based on John McIntosh's free 4D Maze game. The participating persons had to navigate through the path and finally estimate the linear direction back to the starting point. The researchers found that some of the participants were able to mentally integrate their path after some practice in 4D (the lower-dimensional cases were for comparison and for the participants to learn the method).
In culture
Science fiction texts often mention the concept of "dimension" when referring to parallel or alternate universes or other imagined planes of existence. This usage is derived from the idea that to travel to parallel/alternate universes/planes of existence one must travel in a direction/dimension besides the standard ones. In effect, the other universes/planes are just a small distance away from our own, but the distance is in a fourth (or higher) spatial (or non-spatial) dimension, not the standard ones.
One of the most heralded science fiction stories regarding true geometric dimensionality, and often recommended as a starting point for those just starting to investigate such matters, is the 1884 novella Flatland by Edwin A. Abbott. Isaac Asimov, in his foreword to the Signet Classics 1984 edition, described Flatland as "The best introduction one can find into the manner of perceiving dimensions."
The idea of other dimensions was incorporated into many early science fiction stories, appearing prominently, for example, in Miles J. Breuer's The Appendix and the Spectacles (1928) and Murray Leinster's The Fifth-Dimension Catapult (1931); and appeared irregularly in science fiction by the 1940s. Classic stories involving other dimensions include Robert A. Heinlein's —And He Built a Crooked House (1941), in which a California architect designs a house based on a three-dimensional projection of a tesseract; Alan E. Nourse's Tiger by the Tail and The Universe Between (both 1951); and The Ifth of Oofth (1957) by Walter Tevis. Another reference is Madeleine L'Engle's novel A Wrinkle In Time (1962), which uses the fifth dimension as a way of "tesseracting the universe" or "folding" space to move across it quickly. The fourth and fifth dimensions are also key components of the book The Boy Who Reversed Himself by William Sleator.
In philosophy
Immanuel Kant, in 1783, wrote: "That everywhere space (which is not itself the boundary of another space) has three dimensions and that space, in general, cannot have more dimensions is based on the proposition that not more than three lines can intersect at right angles in one point. This proposition cannot at all be shown from concepts, but rests immediately on intuition and indeed on pure intuition a priori because it is apodictically (demonstrably) certain."
"Space has Four Dimensions" is a short story published in 1846 by German philosopher and experimental psychologist Gustav Fechner under the pseudonym "Dr. Mises". The protagonist in the tale is a shadow who is aware of and able to communicate with other shadows, but who is trapped on a two-dimensional surface. According to Fechner, this "shadow-man" would conceive of the third dimension as being one of time. The story bears a strong similarity to the "Allegory of the Cave" presented in Plato's The Republic (c. 380 BC).
Simon Newcomb wrote an article for the Bulletin of the American Mathematical Society in 1898 entitled "The Philosophy of Hyperspace". Linda Dalrymple Henderson coined the term "hyperspace philosophy", used to describe writing that uses higher dimensions to explore metaphysical themes, in her 1983 thesis about the fourth dimension in early-twentieth-century art. Examples of "hyperspace philosophers" include Charles Howard Hinton, the first writer, in 1888, to use the word "tesseract"; and the Russian esotericist P. D. Ouspensky.
Images for kids
See also
 In Spanish: Cuarta dimensión para niños
In Spanish: Cuarta dimensión para niños