Map projection facts for kids
A map projection is a way of showing the surface of a three-dimensional sphere on a flat surface. Such projections are necessary to create maps. The problem with projections is that they change the surface in some way; this is called distorsion. Depending on the purpose of the map, some distorsions may be acceptable. For this reason, there are different map projections that serve different purposes.
Carl Friedrich Gauss showed that is not possible to project the surface of a sphere to a plane, without distorting it. This theorem is known as Theorema egregium today.
To understand the projections, it is easier to imagine a light source, a globe, and another geometric object. The light source shines "a shadow" of each point of the globe onto the geometric object. At the end the surface of the geometric object is unrolled, this yields the map. It is possible to tell the projections apart by the type of helper object used.
- Using a plane gives azimuthal projections.
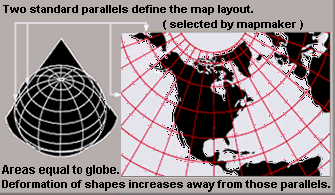
- Using a cone gives conical projections.
- Using a cylinder gives cylindrical ones.
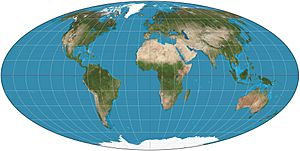
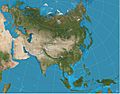
- Cylindrical projections "put the sphere into a cylinder, and then unroll its surface". Examples of these are Equirectangular projection, Mercator projection
- Psedocylindrincal: Same as cylindrical, but only applies to the main meridian and parallels.
Metric properties of maps
Many properties can be measured on the Earth's surface independent of its geography. Some of these properties are:
Map projections can be constructed to preserve at least one of these properties, though only in a limited way for most. Each projection preserves, compromises, or approximates basic metric properties in different ways. The purpose of the map determines which projection should form the base for the map. Because many purposes exist for maps, a diversity of projections have been created to suit those purposes.
Images for kids
-
A medieval depiction of the Ecumene (1482, Johannes Schnitzer, engraver), constructed after the coordinates in Ptolemy's Geography and using his second map projection
-
.
Tissot's Indicatrices on the Mercator projection
-
A stereographic projection is conformal and perspective but not equal area or equidistant.
-
The Gnomonic projection is thought to be the oldest map projection, developed by Thales in the 6th century BC
-
The Robinson projection was adopted by National Geographic magazine in 1988 but abandoned by them in about 1997 for the Winkel tripel.
See also
 In Spanish: Proyección cartográfica para niños
In Spanish: Proyección cartográfica para niños