Karl Weierstrass Facts for Kids

Quick facts for kids Karl Weierstrass
Karl Weierstraß

Born	(1815-10-31)31 October 1815 Ennigerloh, Kingdom of Prussia
Died	19 February 1897(1897-02-19) (aged 81) Berlin, Kingdom of Prussia
Nationality	German
Alma mater	University of Bonn Münster Academy
Awards	PhD (Hon): University of Königsberg (1854) Copley Medal (1895)
Scientific career
Fields	Mathematics
Institutions	Gewerbeinstitut, Friedrich Wilhelm University
Academic advisors	Christoph Gudermann
Doctoral students	Nikolai Bugaev Georg Cantor Georg Frobenius Lazarus Fuchs Wilhelm Killing Johannes Knoblauch Leo Königsberger Ernst Kötter Sofia Kovalevskaya Mathias Lerch Hans von Mangoldt Eugen Netto Adolf Piltz Carl Runge Arthur Schoenflies Friedrich Schottky Hermann Schwarz Ludwig Stickelberger

Karl Theodor Wilhelm Weierstrass (German: Weierstraß [ˈvaɪɐʃtʁaːs]; 31 October 1815 – 19 February 1897) was a German mathematician often cited as the "father of modern analysis". Despite leaving university without a degree, he studied mathematics and trained as a school teacher, eventually teaching mathematics, physics, botany and gymnastics. He later received an honorary doctorate and became professor of mathematics in Berlin.

Among many other contributions, Weierstrass formalized the definition of the continuity of a function, proved the intermediate value theorem and the Bolzano–Weierstrass theorem, and used the latter to study the properties of continuous functions on closed bounded intervals.

Biography
Mathematical contributions
Students
Honours and awards
Selected works
See also

Biography

Weierstrass was born into a Roman Catholic family in Ostenfelde, a village near Ennigerloh, in the Province of Westphalia.

Weierstrass was the son of Wilhelm Weierstrass, a government official, and Theodora Vonderforst both of whom were Catholic Rhinelanders. His interest in mathematics began while he was a gymnasium student at the Theodorianum in Paderborn. He was sent to the University of Bonn upon graduation to prepare for a government position. Because his studies were to be in the fields of law, economics, and finance, he was immediately in conflict with his hopes to study mathematics. He resolved the conflict by paying little heed to his planned course of study but continuing private study in mathematics. The outcome was that he left the university without a degree. He then studied mathematics at the Münster Academy (which was even then famous for mathematics) and his father was able to obtain a place for him in a teacher training school in Münster. Later he was certified as a teacher in that city. During this period of study, Weierstrass attended the lectures of Christoph Gudermann and became interested in elliptic functions.

In 1843 he taught in Deutsch Krone in West Prussia and since 1848 he taught at the Lyceum Hosianum in Braunsberg. Besides mathematics he also taught physics, botany, and gymnastics.

Weierstrass may have had an illegitimate child named Franz with the widow of his friend Carl Wilhelm Borchardt.

After 1850 Weierstrass suffered from a long period of illness, but was able to publish mathematical articles that brought him fame and distinction. The University of Königsberg conferred an honorary doctor's degree on him on 31 March 1854. In 1856 he took a chair at the Gewerbeinstitut in Berlin (an institute to educate technical workers which would later merge with the Bauakademie to form the Technical University of Berlin). In 1864 he became professor at the Friedrich-Wilhelms-Universität Berlin, which later became the Humboldt Universität zu Berlin.

In 1870, at the age of fifty-five, Weierstrass met Sofia Kovalevsky whom he tutored privately after failing to secure her admission to the university. They had a fruitful intellectual, but troubled personal, relationship that "far transcended the usual teacher-student relationship". The misinterpretation of this relationship and Kovalevsky's early death in 1891 was said to have contributed to Weierstrass' later ill-health. He was immobile for the last three years of his life, and died in Berlin from pneumonia.

Mathematical contributions

Soundness of calculus

Weierstrass was interested in the soundness of calculus, and at the time there were somewhat ambiguous definitions of the foundations of calculus so that important theorems could not be proven with sufficient rigour. Although Bolzano had developed a reasonably rigorous definition of a limit as early as 1817 (and possibly even earlier) his work remained unknown to most of the mathematical community until years later, and many mathematicians had only vague definitions of limits and continuity of functions.

The basic idea behind Delta-epsilon proofs is, arguably, first found in the works of Cauchy in the 1820s. Cauchy did not clearly distinguish between continuity and uniform continuity on an interval. Notably, in his 1821 Cours d'analyse, Cauchy argued that the (pointwise) limit of (pointwise) continuous functions was itself (pointwise) continuous, a statement that is false in general. The correct statement is rather that the uniform limit of continuous functions is continuous (also, the uniform limit of uniformly continuous functions is uniformly continuous). This required the concept of uniform convergence, which was first observed by Weierstrass's advisor, Christoph Gudermann, in an 1838 paper, where Gudermann noted the phenomenon but did not define it or elaborate on it. Weierstrass saw the importance of the concept, and both formalized it and applied it widely throughout the foundations of calculus.

The formal definition of continuity of a function, as formulated by Weierstrass, is as follows:

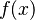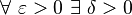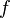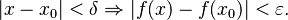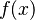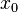$\displaystyle f(x)$ is continuous at $\displaystyle x = x_0$ if $\displaystyle \forall \ \varepsilon > 0\ \exists\ \delta > 0$ such that for every $x$ in the domain of $f$ , $\displaystyle \ |x-x_0| < \delta \Rightarrow |f(x) - f(x_0)| < \varepsilon.$ In simple English, $\displaystyle f(x)$ is continuous at a point $\displaystyle x = x_0$ if for each $x$ close enough to $x_0$ , the function value 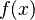$f(x)$ is very close to 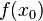$f(x_0)$ , where the "close enough" restriction typically depends on the desired closeness of 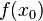$f(x_0)$ to $f(x).$ 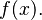Using this definition, he proved the Intermediate Value Theorem. He also proved the Bolzano–Weierstrass theorem and used it to study the properties of continuous functions on closed and bounded intervals.

Calculus of variations

Weierstrass also made advances in the field of calculus of variations. Using the apparatus of analysis that he helped to develop, Weierstrass was able to give a complete reformulation of the theory that paved the way for the modern study of the calculus of variations. Among several axioms, Weierstrass established a necessary condition for the existence of strong extrema of variational problems. He also helped devise the Weierstrass–Erdmann condition, which gives sufficient conditions for an extremal to have a corner along a given extremum and allows one to find a minimizing curve for a given integral.

Other analytical theorems

Stone–Weierstrass theorem
Casorati–Weierstrass theorem
Weierstrass elliptic function
Weierstrass function
Weierstrass M-test
Weierstrass preparation theorem
Lindemann–Weierstrass theorem
Weierstrass factorization theorem
Weierstrass–Enneper parameterization

Students

Edmund Husserl

Honours and awards

The lunar crater Weierstrass and the asteroid 14100 Weierstrass are named after him. Also, there is the Weierstrass Institute for Applied Analysis and Stochastics in Berlin.

Selected works

Zur Theorie der Abelschen Funktionen (1854)
Theorie der Abelschen Funktionen (1856)
Abhandlungen-1, Math. Werke. Bd. 1. Berlin, 1894
Abhandlungen-2, Math. Werke. Bd. 2. Berlin, 1895
Abhandlungen-3, Math. Werke. Bd. 3. Berlin, 1903
Vorl. ueber die Theorie der Abelschen Transcendenten, Math. Werke. Bd. 4. Berlin, 1902
Vorl. ueber Variationsrechnung, Math. Werke. Bd. 7. Leipzig, 1927

Karl Weierstrass facts for kids

Contents