Interpretations of quantum mechanics facts for kids
In quantum mechanics, the mathematical formalism is very difficult to interpret physically. However, there are many ideas about the interpretations and meanings of quantum mechanics. There are no facts to prove any interpretation over the others, but there are some that are more accepted than others.
Background material
Main article: Quantum mechanics
The main ideas of quantum mechanics are the postulates of Schrödinger and Heisenberg. The Schrödinger equation is a partial differential equation that describes the wavefunction of an object. The equation can be given by
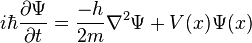
The basic meaning of this equation is that a particle, such as an electron, is not just a point-like particle, but also a type of wave. The philosophical implications will be explored shortly. Another fundamental of quantum mechanics is the Heisenberg uncertainty principle. This bizarre theory is the idea that the position and the momentum of an object cannot both be known. The greater the certainty of the position of an object, the less the certainty of the momentum of the object. The mathematical formulation of this is given by
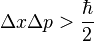
This can further be generalized by stating that
![\Delta X_1\Delta X_2>\frac{[X_1, X_2]}{2i}](/images/math/d/0/9/d094a5faa994c8fab75b2f676d74ec87.png)
Where ![[X_1, X_2]](/images/math/6/d/8/6d8b4cd69dc3e37e44491fdf7e5e9678.png) is the operator of
is the operator of 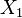 and
and 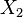 . This law also gives rise to an uncertainty between energy and time, which can be expressed in the same way as the relation between momentum and position.
. This law also gives rise to an uncertainty between energy and time, which can be expressed in the same way as the relation between momentum and position.
Probability waves
Another important fact of quantum mechanics is that the electron behaves in a very weird way. At first, no one really knew what the wavefunction meant physically. Max Born, a theoretical physicist, explained that the wavefunction is a probability wave. In other words, wherever the wave is denser, that is where the particle is most likely found, but it won't necessarily be found there. The way to find the probability (![P_{[a,b]}](/images/math/3/1/0/310b6323d7ea094ed3f4656d4ff02b6f.png) ) of the position of the particle in the region
) of the position of the particle in the region 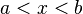 is given by
is given by
![\int_a^b \! |\Psi (x, t)|^2 dx=P_{[a,b]}](/images/math/8/e/f/8efb070492c5d6852da876138c29e775.png)
For example, if ![P_{[a,b]}](/images/math/3/1/0/310b6323d7ea094ed3f4656d4ff02b6f.png) is equal to .5, then there is a 50% chance of finding the particle within that region. This shows us that the location of a particle is probabilistic; one can never say that the particle will definitely be found at a certain point in space, but rather, one can only give the probability of finding the particle within that region.
is equal to .5, then there is a 50% chance of finding the particle within that region. This shows us that the location of a particle is probabilistic; one can never say that the particle will definitely be found at a certain point in space, but rather, one can only give the probability of finding the particle within that region.
See also
 In Spanish: Interpretaciones de la mecánica cuántica para niños
In Spanish: Interpretaciones de la mecánica cuántica para niños

