Zipf's law facts for kids
Zipf's law is an empirical law, formulated using mathematical statistics, named after the linguist George Kingsley Zipf, who first proposed it.
Zipf's law states that given a large sample of words used, the frequency of any word is inversely proportional to its rank in the frequency table. So word number n has a frequency proportional to 1/n.
Thus the most frequent word will occur about twice as often as the second most frequent word, three times as often as the third most frequent word, etc. For example, in one sample of words in the English language, the most frequently occurring word, "the", accounts for nearly 7% of all the words (69,971 out of slightly over 1 million). True to Zipf's Law, the second-place word "of" accounts for slightly over 3.5% of words (36,411 occurrences), followed by "and" (28,852). Only about 135 words are needed to account for half the sample of words in a large sample.
The same relationship occurs in many other rankings, unrelated to language, such as the population ranks of cities in various countries, corporation sizes, income rankings, etc. The appearance of the distribution in rankings of cities by population was first noticed by Felix Auerbach in 1913.
It is not known why Zipf's law holds for most languages.
Images for kids
-
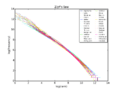
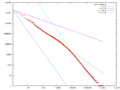
A plot of word frequency in Wikipedia (November 27, 2006). The plot is in log-log coordinates. x is rank of a word in the frequency table; y is the total number of the word's occurrences. Most popular words are "the", "of" and "and", as expected. Zipf's law corresponds to the middle linear portion of the curve, roughly following the green (1/x) line, while the early part is closer to the magenta (1/x0.5) line while the later part is closer to the cyan (1/(k + x)2.0) line. These lines correspond to three distinct parameterizations of the Zipf–Mandelbrot distribution, overall a broken power law with three segments: a head, middle, and tail.
See also
 In Spanish: Ley de Zipf para niños
In Spanish: Ley de Zipf para niños