Twin paradox facts for kids
The twin paradox in physics is a thought experiment (a situation in which a hypothesis, theory, or principle is laid out for the purpose of thinking through its consequences) which involves identical twins, one of whom makes a journey into space in a high-speed rocket and returns home to find that the twin who remained on Earth has aged more. There is still debate as to the resolution of the twin paradox.
Contents
Specific example
Consider a space ship traveling from Earth to the nearest star system: a distance d = 4 light years away, at a speed v = 0.8c (i.e., 80% of the speed of light).
To make the numbers easy, the ship is assumed to attain full speed in a negligible time upon departure (even though it would actually take about 9 months accelerating at 1 g to get up to speed). Similarly, at the end of the outgoing trip, the change in direction needed to start the return trip is assumed to occur in a negligible time. The parties will observe the situation as follows:
Earth perspective
The Earth-based mission control reasons about the journey this way: the round trip will take t = 2d/v = 10 years in Earth time (i.e. everybody who stays on Earth will be 10 years older when the ship returns). The amount of time as measured on the ship's clocks and the aging of the travelers during their trip will be reduced by the factor 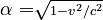 , the reciprocal of the Lorentz factor (time dilation). In this case α = 0.6 and the travelers will have aged only 0.6 × 10 = 6 years when they return.
, the reciprocal of the Lorentz factor (time dilation). In this case α = 0.6 and the travelers will have aged only 0.6 × 10 = 6 years when they return.
Travellers' perspective
The ship's crew members also calculate the particulars of their trip from their perspective. They know that the distant star system and the Earth are moving relative to the ship at speed v during the trip. In their rest frame the distance between the Earth and the star system is α d = 0.6 × 4 = 2.4 light years (length contraction), for both the outward and return journeys. Each half of the journey takes α d / v = 2.4 / 0.8 = 3 years, and the round trip takes twice as long (6 years). Their calculations show that they will arrive home having aged 6 years. The travelers' final calculation about their aging is in complete agreement with the calculations of those on Earth, though they experience the trip quite differently from those who stay at home.
Conclusion
| Event | Earth (years) |
Spaceship (years) |
|---|---|---|
| Departure | 0 | 0 |
| End of outgoing trip = Beginning of ingoing trip |
5 | 3 |
| Arrival | 10 | 6 |
No matter what method they use to predict the clock readings, everybody will agree about them. If twins are born on the day the ship leaves, and one goes on the journey while the other stays on Earth, they will meet again when the traveler is 6 years old and the stay-at-home twin is 10 years old.
Related pages
See also
 In Spanish: Paradoja de los gemelos para niños
In Spanish: Paradoja de los gemelos para niños

