Transformer (deep learning architecture) facts for kids
A transformer is a deep learning architecture developed by Google and based on the multi-head attention mechanism, proposed in a 2017 paper "Attention Is All You Need". Text is converted to numerical representations called tokens, and each token is converted into a vector via looking up from a word embedding table. At each layer, each token is then contextualized within the scope of the context window with other (unmasked) tokens via a parallel multi-head attention mechanism allowing the signal for key tokens to be amplified and less important tokens to be diminished. The transformer paper, published in 2017, is based on the softmax-based attention mechanism proposed by Bahdanau et al. in 2014 for machine translation.
Transformers have the advantage of having no recurrent units, and therefore require less training time than earlier recurrent neural architectures (RNNs) such as long short-term memory (LSTM). Later variations have been widely adopted for training large language models (LLM) on large (language) datasets, such as the Wikipedia corpus and Common Crawl.
Transformers are currently used in large-scale natural language processing, computer vision (vision transformers), audio, multi-modal processing, robotics, and even playing chess. It has also led to the development of pre-trained systems, such as generative pre-trained transformers (GPTs) and BERT (Bidirectional Encoder Representations from Transformers).
History
Timeline
- In 1990, the Elman network, using a recurrent neural network, encoded each word in a training set as a vector, called a word embedding, and the whole vocabulary as a vector database, allowing it to perform such tasks as sequence-predictions that are beyond the power of a simple multilayer perceptron. A shortcoming of the static embeddings was that they didn't differentiate between multiple meanings of homonyms.
- In 1992, the fast weight controller was published by Jürgen Schmidhuber. One network of another neural network through outer products of key vectors and value vectors called FROM and TO. It was later shown to be equivalent to the unnormalized linear Transformer. Schmidhuber used the terminology "learning internal spotlights of attention" in 1993, and now claims it was a precursor to what is now known as the attention mechanism, but Geoffrey Hinton disputes this claim of priority.
- In 1993, the IBM alignment models were used for statistical machine translation.
- In 2001, a one-billion-word large text corpus, scraped from the Internet, referred to as "very very large" at the time, was used for word disambiguation.
- In 2012, AlexNet demonstrated the effectiveness of large neural networks for image recognition, encouraging large artificial neural networks approach instead of older, statistical approaches.
- In 2014, a 380M-parameter seq2seq model for machine translation using two Long short-term Memory (LSTMs) networks was proposed by Sutskever at al. The architecture consists of two parts. The encoder is an LSTM that takes in a sequence of tokens and turns it into a vector. The decoder is another LSTM that converts the vector into a sequence of tokens.
- In 2014, gating proved to be useful in a 130M-parameter seq2seq model, which used a simplified gated recurrent units (GRUs). Bahdanau et al showed that GRUs are neither better nor worse than gated LSTMs.
- In 2014, Bahdanau et al. improved the previous seq2seq model by using an "additive" kind of attention mechanism in-between two LSTM networks. It was, however, not yet the parallelizable (scaled "dot product") kind of attention, later proposed in the 2017 transformer paper.
- In 2015, the relative performance of Global and Local (windowed) attention model architectures were assessed by Luong et al, a mixed attention architecture found to improve on the translations offered by Bahdanau's architecture, while the use of a local attention architecture reduced translation time.
- In 2016, Google Translate gradually replaced the older statistical machine translation approach with the newer neural-networks-based approach that included a seq2seq model combined by LSTM and the "additive" kind of attention mechanism. They achieved a higher level of performance than the statistical approach, which took ten years to develop, in only nine months.
- In 2017, the original (100M-sized) encoder-decoder transformer model with a faster (parallelizable or decomposable) attention mechanism was proposed in the "Attention is all you need" paper. As the model had difficulties converging, it was suggested that the learning rate should be linearly scaled up from 0 to maximal value for the first part of the training (i.e. 2% of the total number of training steps). The intent of the transformer model is to take a seq2seq model and remove its recurrent neural networks, but preserve its additive attention mechanism.
- In the 2018 ELMo paper, a bi-directional LSTM is used to calculate deep contextualized embeddings for each word, improving upon the line of research from bag of words and word2vec.
- In 2018, an encoder-only transformer was used in the (more than 1B-sized) BERT model, improving upon ELMo.
- In 2020, vision transformer and speech-processing convolution-augmented transformer outperformed recurrent neural networks, previously used for vision and speech.
- In 2020, difficulties with converging the original transformer were solved by normalizing layers before (instead of after) multiheaded attention by Xiong et al. This is called pre-LN Transformer.
- In 2023, uni-directional ("autoregressive") transformers were being used in the (more than 100B-sized) GPT-3 and other OpenAI GPT models.
- In 2024, transformers were applied to evaluating chess board positions. Using static evaluation alone (that is, with no Minimax search) it was able to achieve an Elo of 2895, putting it at grandmaster level.
Predecessors
Sequence modelling and generation had been done with plain recurrent neural networks for many years. An early well-cited example was the Elman network (1990). In theory, the information from one token can propagate arbitrarily far down the sequence, but in practice the vanishing-gradient problem leaves the model's state at the end of a long sentence without precise, extractable information about preceding tokens.
One key component of the attention mechanism is to include neurons that multiply the outputs of other neurons. Such neurons were called multiplicative units, and neural networks using multiplicative units were called sigma-pi networks or second-order networks, but they faced high computational complexity. A key breakthrough was LSTM (1995), which incorporated multiplicative units into a recurrent network, as well as other innovations that prevented the vanishing gradient problem, and allowed efficient learning of long-sequence modelling. It became the standard architecture for long sequence modelling until the 2017 publication of Transformers.
However, LSTM did not solve a general problem that recurrent networks usually have, which is that it cannot operate in parallel over all tokens in a sequence. It must operate one at a time from the first token to the last. The fast weight controller (1992) was an early attempt to bypass the difficulty. It used the fast weights architecture, where one neural network outputs the weights of another neural network. It was later shown to be equivalent to the linear Transformer without normalization.
Recurrent attention
In 2014, an attention mechanism was introduced to seq2seq models (using gated recurrent units, a variant of LSTM) for machine translation. It was introduced to solve a specific issue encountered in seq2seq. In seq2seq, the input is processed sequentially by one recurrent network into a fixed-size output vector, which was then processed by another recurrent network into an output. If the input is long, then the output vector would not be able to contain all relevant information, and the output quality degrades.
The idea of attention mechanism in recurrent networks is to use all outputs of the first network, not just its last output. The second network at each step uses an attention mechanism to combine them linearly, then processes it further.
Previously seq2seq had no attention mechanism, and the state vector is accessible only after the last word of the source text was processed. Although in theory such a vector retains the information about the whole original sentence, in practice the information is poorly preserved. This is because seq2seq models have difficulty modelling long-distance dependencies. Reversing the input sentence improved seq2seq translation. With an attention mechanism, the network can model long-distance dependencies more easily.
Attention
Seq2seq models with attention still suffered from the same issue with recurrent networks, which is that they are hard to parallelize, which prevented them to be accelerated on GPUs. In 2016, decomposable attention applied attention mechanism to the feedforward network, which are easy to parallelize.
In 2017, Vaswani et al. also proposed replacing recurrent neural networks with self-attention and started the effort to evaluate that idea. Transformers, using an attention mechanism, processing all tokens simultaneously, calculated "soft" weights between them in successive layers. Since the attention mechanism only uses information about other tokens from lower layers, it can be computed for all tokens in parallel, which leads to improved training speed.
Training
Methods for stabilizing training
The plain transformer architecture had difficulty converging. In the original paper the authors recommended using learning rate warmup. That is, the learning rate should linearly scale up from 0 to maximal value for the first part of the training (usually recommended to be 2% of the total number of training steps), before decaying again.
A 2020 paper found that using layer normalization before (instead of after) multiheaded attention and feedforward layers stabilizes training, not requiring learning rate warmup.
Pretrain-finetune
Transformers typically undergo self-supervised learning involving unsupervised pretraining followed by supervised fine-tuning. Pretraining is typically done on a larger dataset than fine-tuning, due to the limited availability of labeled training data. Tasks for pretraining and fine-tuning commonly include:
- language modeling
- next-sentence prediction
- question answering
- reading comprehension
- sentiment analysis
- paraphrasing
The T5 transformer report documents a large number of pretraining tasks. Some examples are:
- restoring corrupted text:
Thank you <X> me to your party <Y> week.-><X> for inviting <Y> last <Z>where the<Z>means "end of output". - translation:
translate English to German: That is good.->Das ist gut.. - judging the grammatical acceptability of a sentence (CoLA sentence):
The course is jumping well.->not acceptable.
Applications
The transformer has had great success in natural language processing (NLP), for example the tasks of machine translation and time series prediction. Many large language models such as GPT-2, GPT-3, GPT-4, Claude, BERT, XLNet, RoBERTa and ChatGPT demonstrate the ability of transformers to perform a wide variety of such NLP-related tasks, and have the potential to find real-world applications. These may include:
- machine translation
- document summarization
- document generation
- named entity recognition (NER)
- biological sequence analysis
- writing computer code based on requirements expressed in natural language.
- video understanding.
In addition to the NLP applications, it has also been successful in other fields, such as computer vision, or the protein folding applications (such as AlphaFold).
As an illustrative example, Ithaca is an encoder-only transformer with three output heads. It takes as input ancient Greek inscription as sequences of characters, but with illegible characters replaced with "-". Its three output heads respectively outputs probability distributions over Greek characters, location of inscription, and date of inscription.
Implementations
The transformer model has been implemented in standard deep learning frameworks such as TensorFlow and PyTorch.
Transformers is a library produced by Hugging Face that supplies transformer-based architectures and pretrained models.
Architecture
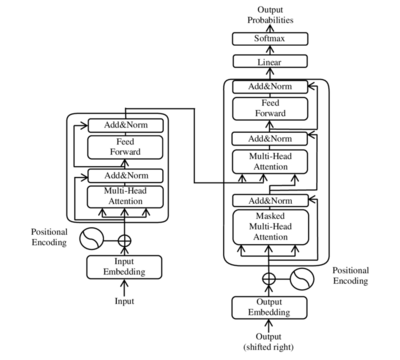
All transformers have the same primary components:
- Tokenizers, which convert text into tokens.
- A single embedding layer, which converts tokens and positions of the tokens into vector representations.
- Transformer layers, which carry out repeated transformations on the vector representations, extracting more and more linguistic information. These consist of alternating attention and feedforward layers.
- (optional) Un-embedding layer, which converts the final vector representations back to a probability distribution over the tokens.
Transformer layers can be one of two types, encoder and decoder. In the original paper both of them were used, while later models included only one type of them. BERT is an example of an encoder-only model; GPT are decoder-only models.
Input
The input text is parsed into tokens by a tokenizer, most often a byte pair encoding tokenizer, and each token is converted into a vector via looking up from a word embedding table. Then, positional information of the token is added to the word embedding.
Encoder-decoder architecture
Like earlier seq2seq models, the original transformer model used an encoder-decoder architecture. The encoder consists of encoding layers that process the input tokens iteratively one layer after another, while the decoder consists of decoding layers that iteratively process the encoder's output as well as the decoder output's tokens so far.
The function of each encoder layer is to generate contextualized token representations, where each representation corresponds to a token that "mixes" information from other input tokens via self-attention mechanism. Each decoder layer contains two attention sublayers: (1) cross-attention for incorporating the output of encoder (contextualized input token representations), and (2) self-attention for "mixing" information among the input tokens to the decoder (i.e., the tokens generated so far during inference time).
Both the encoder and decoder layers have a feed-forward neural network for additional processing of the outputs and contain residual connections and layer normalization steps.
Scaled dot-product attention
The transformer building blocks are scaled dot-product attention units. For each attention unit, the transformer model learns three weight matrices: the query weights 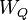 , the key weights
, the key weights 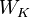 , and the value weights
, and the value weights  . For each token
. For each token 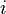 , the input token representation
, the input token representation 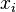 is multiplied with each of the three weight matrices to produce a query vector
is multiplied with each of the three weight matrices to produce a query vector 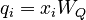 , a key vector
, a key vector 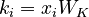 , and a value vector
, and a value vector  . Attention weights are calculated using the query and key vectors: the attention weight
. Attention weights are calculated using the query and key vectors: the attention weight 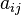 from token
from token 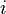 to token
to token 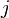 is the dot product between
is the dot product between  and
and 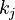 . The attention weights are divided by the square root of the dimension of the key vectors,
. The attention weights are divided by the square root of the dimension of the key vectors, 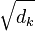 , which stabilizes gradients during training, and passed through a softmax which normalizes the weights. The fact that
, which stabilizes gradients during training, and passed through a softmax which normalizes the weights. The fact that 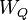 and
and 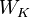 are different matrices allows attention to be non-symmetric: if token
are different matrices allows attention to be non-symmetric: if token 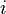 attends to token
attends to token 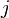 (i.e.
(i.e. 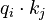 is large), this does not necessarily mean that token
is large), this does not necessarily mean that token 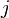 will attend to token
will attend to token 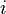 (i.e.
(i.e. 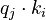 could be small). The output of the attention unit for token
could be small). The output of the attention unit for token 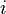 is the weighted sum of the value vectors of all tokens, weighted by
is the weighted sum of the value vectors of all tokens, weighted by 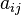 , the attention from token
, the attention from token 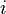 to each token.
to each token.
The attention calculation for all tokens can be expressed as one large matrix calculation using the softmax function, which is useful for training due to computational matrix operation optimizations that quickly compute matrix operations. The matrices 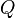 ,
, 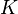 and
and 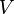 are defined as the matrices where the
are defined as the matrices where the 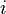 th rows are vectors
th rows are vectors  ,
, 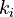 , and
, and 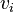 respectively. Then we can represent the attention as
respectively. Then we can represent the attention as

where softmax is taken over the horizontal axis.
Multi-head attention
One set of  matrices is called an attention head, and each layer in a transformer model has multiple attention heads. While each attention head attends to the tokens that are relevant to each token, multiple attention heads allow the model to do this for different definitions of "relevance". In addition, the influence field representing relevance can become progressively dilated in successive layers. Many transformer attention heads encode relevance relations that are meaningful to humans. For example, some attention heads can attend mostly to the next word, while others mainly attend from verbs to their direct objects. The computations for each attention head can be performed in parallel, which allows for fast processing. The outputs for the attention layer are concatenated to pass into the feed-forward neural network layers.
matrices is called an attention head, and each layer in a transformer model has multiple attention heads. While each attention head attends to the tokens that are relevant to each token, multiple attention heads allow the model to do this for different definitions of "relevance". In addition, the influence field representing relevance can become progressively dilated in successive layers. Many transformer attention heads encode relevance relations that are meaningful to humans. For example, some attention heads can attend mostly to the next word, while others mainly attend from verbs to their direct objects. The computations for each attention head can be performed in parallel, which allows for fast processing. The outputs for the attention layer are concatenated to pass into the feed-forward neural network layers.
Concretely, let the multiple attention heads be indexed by 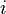 , then we have
, then we have![{\displaystyle \text{MultiheadedAttention}(Q, K, V) = \text{Concat}_{i \in [\# heads]}(\text{Attention}(XW^Q_i, XW^K_i, XW^V_i)) W^O}](/images/math/7/f/f/7ff13fb15c4e1241746f36a18110f0a9.png) where the matrix
where the matrix 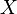 is the concatenation of word embeddings, and the matrices
is the concatenation of word embeddings, and the matrices 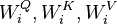 are "projection matrices" owned by individual attention head
are "projection matrices" owned by individual attention head 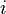 , and
, and 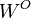 is a final projection matrix owned by the whole multi-headed attention head.
is a final projection matrix owned by the whole multi-headed attention head.
Masked attention
It may be necessary to cut out attention links between some word-pairs. For example, the decoder, when decoding for the token position  , should not have access to the token at position
, should not have access to the token at position 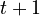 . This may be accomplished before the softmax stage by adding a mask matrix
. This may be accomplished before the softmax stage by adding a mask matrix 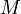 that is
that is 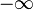 at entries where the attention link must be cut, and
at entries where the attention link must be cut, and 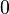 at other places:
at other places: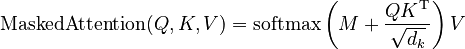 For example, the following mask matrix is used in autoregressive modeling:
For example, the following mask matrix is used in autoregressive modeling: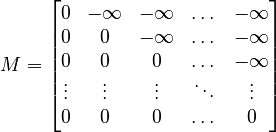 In words, it means that each token can pay attention to itself, and every token before it, but not any after it.
In words, it means that each token can pay attention to itself, and every token before it, but not any after it.
Encoder
Each encoder consists of two major components: a self-attention mechanism and a feed-forward neural network. The self-attention mechanism accepts input encodings from the previous encoder and weights their relevance to each other to generate output encodings. The feed-forward neural network further processes each output encoding individually. These output encodings are then passed to the next encoder as its input, as well as to the decoders.
The first encoder takes positional information and embeddings of the input sequence as its input, rather than encodings. The positional information is necessary for the transformer to make use of the order of the sequence, because no other part of the transformer makes use of this.
The encoder is bidirectional. Attention can be placed on tokens before and after the current token. Tokens are used instead of words to account for polysemy.
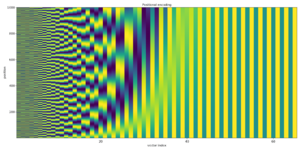
Positional encoding
A positional encoding is a fixed-size vector representation that encapsulates the relative positions of tokens within a target sequence: it provides the transformer model with information about where the words are in the input sequence.
The positional encoding is defined as a function of type 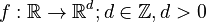 , where
, where 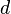 is a positive even integer. The full positional encoding – as defined in the original paper – is given by the equation:
is a positive even integer. The full positional encoding – as defined in the original paper – is given by the equation: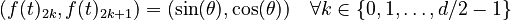 where
where 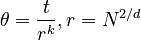 .
.
Here, 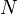 is a free parameter that should be significantly larger than the biggest
is a free parameter that should be significantly larger than the biggest 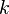 that would be input into the positional encoding function. In the original paper, the authors chose
that would be input into the positional encoding function. In the original paper, the authors chose 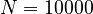 .
.
The function is in a simpler form when written as a complex function of type 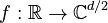
 where
where 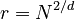 .
.
The main reason the authors chose this as the positional encoding function is that it allows one to perform shifts as linear transformations: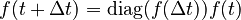 where
where 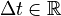 is the distance one wishes to shift. This allows the transformer to take any encoded position, and find the encoding of the position n-steps-ahead or n-steps-behind, by a matrix multiplication.
is the distance one wishes to shift. This allows the transformer to take any encoded position, and find the encoding of the position n-steps-ahead or n-steps-behind, by a matrix multiplication.
By taking a linear sum, any convolution can also be implemented as linear transformations: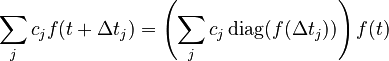 for any constants
for any constants  . This allows the transformer to take any encoded position and find a linear sum of the encoded locations of its neighbors. This sum of encoded positions, when fed into the attention mechanism, would create attention weights on its neighbors, much like what happens in a convolutional neural network language model. In the author's words, "we hypothesized it would allow the model to easily learn to attend by relative position."
. This allows the transformer to take any encoded position and find a linear sum of the encoded locations of its neighbors. This sum of encoded positions, when fed into the attention mechanism, would create attention weights on its neighbors, much like what happens in a convolutional neural network language model. In the author's words, "we hypothesized it would allow the model to easily learn to attend by relative position."
In typical implementations, all operations are done over the real numbers, not the complex numbers, but since complex multiplication can be implemented as real 2-by-2 matrix multiplication, this is a mere notational difference.
Decoder
Each decoder consists of three major components: a self-attention mechanism, an attention mechanism over the encodings, and a feed-forward neural network. The decoder functions in a similar fashion to the encoder, but an additional attention mechanism is inserted which instead draws relevant information from the encodings generated by the encoders. This mechanism can also be called the encoder-decoder attention.
Like the first encoder, the first decoder takes positional information and embeddings of the output sequence as its input, rather than encodings. The transformer must not use the current or future output to predict an output, so the output sequence must be partially masked to prevent this reverse information flow. This allows for autoregressive text generation. For all attention heads, attention can't be placed on following tokens. The last decoder is followed by a final linear transformation and softmax layer, to produce the output probabilities over the vocabulary.
All members of OpenAI's GPT series have a decoder-only architecture.
Terminology
In large language models, the terminology is somewhat different than the terminology used in the original Transformer paper:
- "encoder only": full encoder, full decoder.
- "encoder-decoder": full encoder, autoregressive decoder.
- "decoder only": autoregressive encoder, autoregressive decoder.
Here "autoregressive" means that a mask is inserted in the attention head to zero out all attention from one token to all tokens following it, as described in the "masked attention" section.
Generally, Transformer-based language models are of two types: causal (or "autoregressive") and masked. The GPT series is causal and decoder only. BERT is masked and encoder only. The T5 series is encoder-decoder, with a full encoder and autoregressive decoder.
Subsequent work
Alternative activation functions
The original transformer uses ReLU activation function. Other activation functions were developed, such as SwiGLU.
Alternative positional encodings
Transformers may use other positional encoding methods than sinusoidal.
RoPE
RoPE (rotary positional embedding), is best explained by considering a list of 2-dimensional vectors ![[(x^{(1)}_1, x^{(2)}_1), (x^{(1)}_2, x^{(2)}_2), (x^{(1)}_3, x^{(2)}_3), ...]](/images/math/9/c/6/9c660540cbc3d4ea1ae2eb3660aeb1b4.png) . Now pick some angle
. Now pick some angle 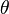 . Then RoPE encoding is
. Then RoPE encoding is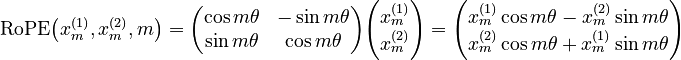 Equivalently, if we write the 2-dimensional vectors as complex numbers
Equivalently, if we write the 2-dimensional vectors as complex numbers 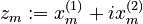 , then RoPE encoding is just multiplication by an angle:
, then RoPE encoding is just multiplication by an angle: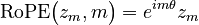 For a list of
For a list of 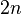 -dimensional vectors, a RoPE encoder is defined by a sequence of angles
-dimensional vectors, a RoPE encoder is defined by a sequence of angles 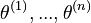 . Then the RoPE encoding is applied to each pair of coordinates.
. Then the RoPE encoding is applied to each pair of coordinates.
The benefit of RoPE is that the dot-product between two vectors depends on their relative location only:
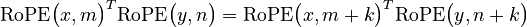 for any integer
for any integer 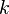 .
.
ALiBi
ALiBi (Attention with Linear Biases) is not a replacement for the positional encoder on the original transformer. Instead, it is an additional positional encoder that is directly plugged into the attention mechanism. Specifically, the ALiBi attention mechanism is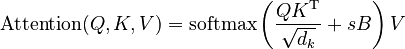 Here,
Here,  is a real number ("scalar"), and
is a real number ("scalar"), and 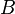 is the linear bias matrix defined by
is the linear bias matrix defined by in other words,
in other words, 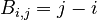 .
.
ALiBi allows pretraining on short context windows, then finetuning on longer context windows. Since it is directly plugged into the attention mechanism, it can be combined with any positional encoder that is plugged into the "bottom" of the entire network (which is where the sinusoidal encoder on the original transformer, as well as RoPE and many others, are located).
Relative Position Encodings
Relative Position Encodings is similar to ALiBi, but more generic: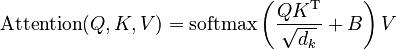 where
where 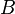 is a Toeplitz matrix, that is,
is a Toeplitz matrix, that is, 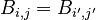 whenever
whenever 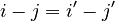 .
.
Efficient implementation
FlashAttention
FlashAttention is an algorithm that implements the transformer attention mechanism efficiently on a GPU. It performs matrix multiplications in blocks, such that each block fits within the cache of a GPU, and by careful management of the blocks it minimizes data copying between GPU caches (as data movement is slow).
An improved version, FlashAttention-2, was developed to cater to the rising demand for language models capable of handling longer context lengths. It offers enhancements in work partitioning and parallelism, enabling it to achieve up to 230 TFLOPs/s on A100 GPUs (FP16/BF16), a 2x speed increase over the original FlashAttention.
Key advancements in FlashAttention-2 include the reduction of non-matmul FLOPs, improved parallelism over the sequence length dimension, better work partitioning between GPU warps, and added support for head dimensions up to 256 and multi-query attention (MQA) and grouped-query attention (GQA).
Benchmarks revealed FlashAttention-2 to be up to 2x faster than FlashAttention and up to 9x faster than a standard attention implementation in PyTorch. Future developments include optimization for new hardware like H100 GPUs and new data types like FP8.
Multi-Query Attention
Multi-Query Attention changes the multiheaded attention mechanism. Whereas normally,
![{\displaystyle \text{MultiheadedAttention}(Q, K, V) = \text{Concat}_{i \in [\# heads]}\left(\text{Attention}(XW^Q_i, XW^K_i, XW^V_i)\right) W^O}](/images/math/8/d/a/8daa6617be74889a97667c099c8071f4.png) with Multi-Query Attention, there is just one
with Multi-Query Attention, there is just one  , thus:
, thus:
![{\displaystyle \text{MultiQueryAttention}(Q, K, V) = \text{Concat}_{i \in [\# heads]}\left(\text{Attention}(XW^Q_i, XW^K, XW^V)\right) W^O}](/images/math/8/3/4/8341772a6127173ef89b6356b20754df.png)
This has a neutral effect on model quality and training speed, but increases inference speed.
Caching
When an autoregressive transformer is used for inference, such as generating text, the query vector is different at each step, but the already-computed key and value vectors are always the same. The KV caching method saves the computed key and value vectors at each attention block, so that they are not recomputed at each new token. PagedAttention applies memory paging to KV caching.
If a transformer is used with a baked-in prompt, such as ["You are a customer support agent..."], then the key and value vectors can be computed for the prompt, and saved on disk. The saving in compute is significant when the model is used for many short interactions, such as in online chatbots.
Speculative decoding
Transformers are used in large language models for autoregressive sequence generation: generating a stream of text, one token at a time. However, in most settings, decoding from language models is memory-bound, meaning that we have spare compute power available. Speculative decoding uses this spare compute power by computing several tokens in parallel. Similarly to speculative execution in CPUs, future tokens are computed concurrently, by speculating on the value of previous tokens, and are later discarded if it turns out the speculation was incorrect.
Specifically, consider a transformer model like GPT-3 with a context window size of 512. To generate an entire context window autoregressively with greedy decoding, it must be run for 512 times, each time generating a token 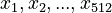 . However, if we had some educated guess for the values of these tokens, we could verify all of them in parallel, in one run of the model, by checking that each
. However, if we had some educated guess for the values of these tokens, we could verify all of them in parallel, in one run of the model, by checking that each 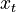 is indeed the token with the largest log-likelihood in the
is indeed the token with the largest log-likelihood in the  -th output.
-th output.
In speculative decoding, a smaller model or some other simple heuristic is used to generate a few speculative tokens that are subsequently verified by the larger model. For example, suppose a small model generated four speculative tokens: 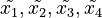 . These tokens are run through the larger model, and only
. These tokens are run through the larger model, and only 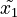 and
and  are accepted. The same run of the large model already generated a new token
are accepted. The same run of the large model already generated a new token 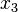 to replace
to replace 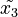 , and
, and 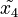 is completely discarded. The process then repeats (starting from the 4th token) until all tokens are generated.
is completely discarded. The process then repeats (starting from the 4th token) until all tokens are generated.
For non-greedy decoding, similar ideas apply, except the speculative tokens are accepted or rejected stochastically, in a way that guarantees the final output distribution is the same as if speculative decoding was not used.
Sub-quadratic transformers
Training transformer-based architectures can be expensive, especially for long inputs. Alternative architectures include the Reformer (which reduces the computational load from  to
to  ), or models like ETC/BigBird (which can reduce it to
), or models like ETC/BigBird (which can reduce it to  ) where
) where 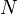 is the length of the sequence. This is done using locality-sensitive hashing and reversible layers.
is the length of the sequence. This is done using locality-sensitive hashing and reversible layers.
Ordinary transformers require a memory size that is quadratic in the size of the context window. Attention-free transformers reduce this to a linear dependence while still retaining the advantages of a transformer by linking the key to the value.
Long Range Arena (2020) is a standard benchmark for comparing the behavior of transformer architectures over long inputs.
Random Feature Attention (2021) uses Fourier random features:![{\displaystyle \varphi(x) = \frac{1}{\sqrt D}[\cos\langle w_1, x\rangle, \sin\langle w_1, x\rangle, \cdots \cos\langle w_D, x\rangle, \sin\langle w_D, x\rangle]^T}](/images/math/1/d/5/1d56a5de24275bc9a565b0bbe3bfc928.png) where
where 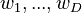 are independent samples from the normal distribution
are independent samples from the normal distribution 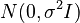 . This choice of parameters satisfy
. This choice of parameters satisfy ![\mathbb E[\langle \varphi(x), \varphi(y)\rangle] = e^{-\frac{\|x-y\|^2}{2\sigma^2}}](/images/math/b/c/8/bc84a4b9ef8aae1386be54570ee65792.png) , or
, or ![{\displaystyle e^{\langle x, y\rangle/\sigma^2} = \mathbb E[\langle e^{\|x\|^2/2\sigma^2} \varphi(x), e^{\|y\|^2/2\sigma^2}\varphi(y)\rangle] \approx \langle e^{\|x\|^2/2\sigma^2} \varphi(x), e^{\|y\|^2/2\sigma^2}\varphi(y)\rangle }](/images/math/2/6/6/266963af06f51be8dd314897edfd97d6.png) Consequently, the one-headed attention, with one query, can be written as
Consequently, the one-headed attention, with one query, can be written as 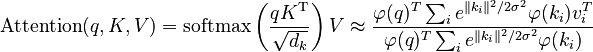 where
where 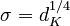 . Similarly for multiple queries, and for multiheaded attention.
. Similarly for multiple queries, and for multiheaded attention.
This approximation can be computed in linear time, as we can compute the matrix  first, then multiply it with the query. In essence, we have managed to obtain a more precise version of
first, then multiply it with the query. In essence, we have managed to obtain a more precise version of 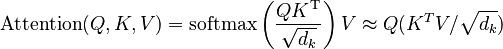
Performer (2022) uses the same Random Feature Attention, but  are first independently sampled from the normal distribution
are first independently sampled from the normal distribution 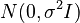 , then they are Gram-Schmidt processed.
, then they are Gram-Schmidt processed.
Multimodality
Transformers can also be used/adapted for modalities (input or output) beyond just text, usually by finding a way to "tokenize" the modality.
Vision transformers adapt the transformer to computer vision by breaking down input images as a series of patches, turning them into vectors, and treating them like tokens in a standard transformer.
Conformer and later Whisper follow the same pattern for speech recognition, first turning the speech signal into a spectrogram, which is then treated like an image, i.e. broken down into a series of patches, turned into vectors and treated like tokens in a standard transformer.
Perceivers by Andrew Jaegle et al. (2021) can learn from large amounts of heterogeneous data.
Regarding image outputs, Peebles et al introduced a diffusion transformer (DiT) which facilitates use of the transformer architecture for diffusion-based image production. Also, Google released a transformer-centric image generator called "Muse" based on parallel decoding and masked generative transformer technology. (Transformers played a less-central role with prior image-producing technologies, albeit still a significant one.)
See also
- Perceiver
- BERT (language model)
- GPT-3
- GPT-4
- ChatGPT
- Wu Dao
- Vision transformer
- BLOOM (language model)