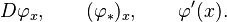Tangent space facts for kids
In mathematics, the tangent space of a manifold is a generalization of tangent lines to curves in two-dimensional space and tangent planes to surfaces in three-dimensional space in higher dimensions. In the context of physics the tangent space to a manifold at a point can be viewed as the space of possible velocities for a particle moving on the manifold.
Informal description

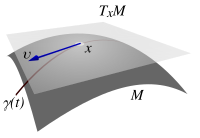
 on a sphere. A vector in this tangent space represents a possible velocity (of something moving on the sphere) at
on a sphere. A vector in this tangent space represents a possible velocity (of something moving on the sphere) at  . After moving in that direction to a nearby point, the velocity would then be given by a vector in the tangent space of that point—a different tangent space that is not shown.
. After moving in that direction to a nearby point, the velocity would then be given by a vector in the tangent space of that point—a different tangent space that is not shown.In differential geometry, one can attach to every point  of a differentiable manifold a tangent space—a real vector space that intuitively contains the possible directions in which one can tangentially pass through
of a differentiable manifold a tangent space—a real vector space that intuitively contains the possible directions in which one can tangentially pass through  . The elements of the tangent space at
. The elements of the tangent space at  are called the tangent vectors at
are called the tangent vectors at  . This is a generalization of the notion of a vector, based at a given initial point, in a Euclidean space. The dimension of the tangent space at every point of a connected manifold is the same as that of the manifold itself.
. This is a generalization of the notion of a vector, based at a given initial point, in a Euclidean space. The dimension of the tangent space at every point of a connected manifold is the same as that of the manifold itself.
For example, if the given manifold is a 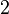 -sphere, then one can picture the tangent space at a point as the plane that touches the sphere at that point and is perpendicular to the sphere's radius through the point. More generally, if a given manifold is thought of as an embedded submanifold of Euclidean space, then one can picture a tangent space in this literal fashion. This was the traditional approach toward defining parallel transport. Many authors in differential geometry and general relativity use it. More strictly, this defines an affine tangent space, which is distinct from the space of tangent vectors described by modern terminology.
-sphere, then one can picture the tangent space at a point as the plane that touches the sphere at that point and is perpendicular to the sphere's radius through the point. More generally, if a given manifold is thought of as an embedded submanifold of Euclidean space, then one can picture a tangent space in this literal fashion. This was the traditional approach toward defining parallel transport. Many authors in differential geometry and general relativity use it. More strictly, this defines an affine tangent space, which is distinct from the space of tangent vectors described by modern terminology.
In algebraic geometry, in contrast, there is an intrinsic definition of the tangent space at a point of an algebraic variety 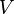 that gives a vector space with dimension at least that of
that gives a vector space with dimension at least that of 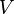 itself. The points
itself. The points 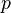 at which the dimension of the tangent space is exactly that of
at which the dimension of the tangent space is exactly that of 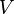 are called non-singular points; the others are called singular points. For example, a curve that crosses itself does not have a unique tangent line at that point. The singular points of
are called non-singular points; the others are called singular points. For example, a curve that crosses itself does not have a unique tangent line at that point. The singular points of 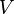 are those where the "test to be a manifold" fails. See Zariski tangent space.
are those where the "test to be a manifold" fails. See Zariski tangent space.
Once the tangent spaces of a manifold have been introduced, one can define vector fields, which are abstractions of the velocity field of particles moving in space. A vector field attaches to every point of the manifold a vector from the tangent space at that point, in a smooth manner. Such a vector field serves to define a generalized ordinary differential equation on a manifold: A solution to such a differential equation is a differentiable curve on the manifold whose derivative at any point is equal to the tangent vector attached to that point by the vector field.
All the tangent spaces of a manifold may be "glued together" to form a new differentiable manifold with twice the dimension of the original manifold, called the tangent bundle of the manifold.
Formal definitions
The informal description above relies on a manifold's ability to be embedded into an ambient vector space 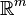 so that the tangent vectors can "stick out" of the manifold into the ambient space. However, it is more convenient to define the notion of a tangent space based solely on the manifold itself.
so that the tangent vectors can "stick out" of the manifold into the ambient space. However, it is more convenient to define the notion of a tangent space based solely on the manifold itself.
There are various equivalent ways of defining the tangent spaces of a manifold. While the definition via the velocity of curves is intuitively the simplest, it is also the most cumbersome to work with. More elegant and abstract approaches are described below.
Definition via tangent curves
In the embedded-manifold picture, a tangent vector at a point  is thought of as the velocity of a curve passing through the point
is thought of as the velocity of a curve passing through the point  . We can therefore define a tangent vector as an equivalence class of curves passing through
. We can therefore define a tangent vector as an equivalence class of curves passing through  while being tangent to each other at
while being tangent to each other at  .
.
Suppose that 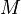 is a
is a  differentiable manifold (with smoothness
differentiable manifold (with smoothness 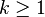 ) and that
) and that 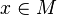 . Pick a coordinate chart
. Pick a coordinate chart 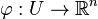 , where
, where 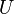 is an open subset of
is an open subset of 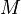 containing
containing  . Suppose further that two curves
. Suppose further that two curves 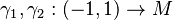 with
with  are given such that both
are given such that both 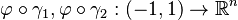 are differentiable in the ordinary sense (we call these differentiable curves initialized at
are differentiable in the ordinary sense (we call these differentiable curves initialized at  ). Then
). Then 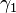 and
and 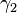 are said to be equivalent at
are said to be equivalent at 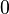 if and only if the derivatives of
if and only if the derivatives of  and
and  at
at 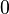 coincide. This defines an equivalence relation on the set of all differentiable curves initialized at
coincide. This defines an equivalence relation on the set of all differentiable curves initialized at  , and equivalence classes of such curves are known as tangent vectors of
, and equivalence classes of such curves are known as tangent vectors of 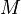 at
at  . The equivalence class of any such curve
. The equivalence class of any such curve 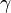 is denoted by
is denoted by  . The tangent space of
. The tangent space of 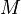 at
at  , denoted by
, denoted by 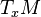 , is then defined as the set of all tangent vectors at
, is then defined as the set of all tangent vectors at  ; it does not depend on the choice of coordinate chart
; it does not depend on the choice of coordinate chart 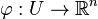 .
.
To define vector-space operations on 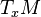 , we use a chart
, we use a chart 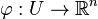 and define a map
and define a map 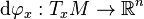 by
by ![{\textstyle {\mathrm{d}{\varphi}_{x}}(\gamma'(0)) := \left. \frac{\mathrm{d}}{\mathrm{d}{t}} [(\varphi \circ \gamma)(t)] \right|_{t = 0}, }](/images/math/3/9/1/39134081be1063f6bbb4213793953888.png) where
where 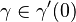 . The map
. The map 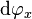 turns out to be bijective and may be used to transfer the vector-space operations on
turns out to be bijective and may be used to transfer the vector-space operations on 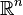 over to
over to 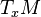 , thus turning the latter set into an
, thus turning the latter set into an 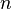 -dimensional real vector space. Again, one needs to check that this construction does not depend on the particular chart
-dimensional real vector space. Again, one needs to check that this construction does not depend on the particular chart 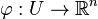 and the curve
and the curve 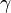 being used, and in fact it does not.
being used, and in fact it does not.
Definition via derivations
Suppose now that 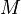 is a
is a 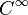 manifold. A real-valued function
manifold. A real-valued function 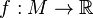 is said to belong to
is said to belong to 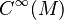 if and only if for every coordinate chart
if and only if for every coordinate chart 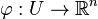 , the map
, the map ![f \circ \varphi^{- 1}: \varphi[U] \subseteq \mathbb{R}^{n} \to \mathbb{R}](/images/math/6/c/8/6c8b0ec0dd012ad59c3f44f11d5e2da6.png) is infinitely differentiable. Note that
is infinitely differentiable. Note that 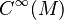 is a real associative algebra with respect to the pointwise product and sum of functions and scalar multiplication.
is a real associative algebra with respect to the pointwise product and sum of functions and scalar multiplication.
A derivation at 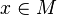 is defined as a linear map
is defined as a linear map 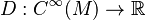 that satisfies the Leibniz identity
that satisfies the Leibniz identity 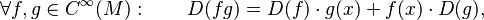 which is modeled on the product rule of calculus.
which is modeled on the product rule of calculus.
(For every identically constant function  it follows that
it follows that 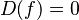 ).
).
Denote 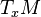 the set of all derivations at
the set of all derivations at 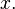 Setting
Setting
 and
and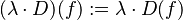
turns 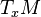 into a vector space.
into a vector space.
Generalizations
Generalizations of this definition are possible, for instance, to complex manifolds and algebraic varieties. However, instead of examining derivations 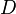 from the full algebra of functions, one must instead work at the level of germs of functions. The reason for this is that the structure sheaf may not be fine for such structures. For example, let
from the full algebra of functions, one must instead work at the level of germs of functions. The reason for this is that the structure sheaf may not be fine for such structures. For example, let 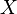 be an algebraic variety with structure sheaf
be an algebraic variety with structure sheaf 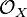 . Then the Zariski tangent space at a point
. Then the Zariski tangent space at a point 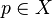 is the collection of all
is the collection of all  -derivations
-derivations 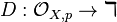 , where
, where  is the ground field and
is the ground field and 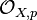 is the stalk of
is the stalk of 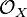 at
at 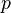 .
.
Equivalence of the definitions
For 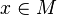 and a differentiable curve
and a differentiable curve 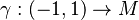 such that
such that 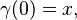 define
define 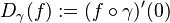 (where the derivative is taken in the ordinary sense because
(where the derivative is taken in the ordinary sense because  is a function from
is a function from 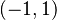 to
to 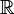 ). One can ascertain that
). One can ascertain that 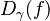 is a derivation at the point
is a derivation at the point 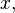 and that equivalent curves yield the same derivation. Thus, for an equivalence class
and that equivalent curves yield the same derivation. Thus, for an equivalence class 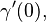 we can define
we can define 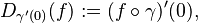 where the curve
where the curve 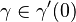 has been chosen arbitrarily. The map
has been chosen arbitrarily. The map  is a vector space isomorphism between the space of the equivalence classes
is a vector space isomorphism between the space of the equivalence classes  and that of the derivations at the point
and that of the derivations at the point 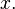
Definition via cotangent spaces
Again, we start with a 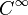 manifold
manifold 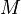 and a point
and a point 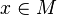 . Consider the ideal
. Consider the ideal 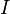 of
of 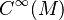 that consists of all smooth functions
that consists of all smooth functions 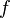 vanishing at
vanishing at  , i.e.,
, i.e., 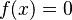 . Then
. Then 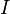 and
and 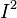 are both real vector spaces, and the quotient space
are both real vector spaces, and the quotient space 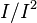 can be shown to be isomorphic to the cotangent space
can be shown to be isomorphic to the cotangent space 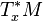 through the use of Taylor's theorem. The tangent space
through the use of Taylor's theorem. The tangent space  may then be defined as the dual space of
may then be defined as the dual space of 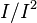 .
.
While this definition is the most abstract, it is also the one that is most easily transferable to other settings, for instance, to the varieties considered in algebraic geometry.
If 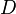 is a derivation at
is a derivation at  , then
, then 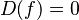 for every
for every 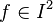 , which means that
, which means that 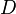 gives rise to a linear map
gives rise to a linear map 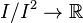 . Conversely, if
. Conversely, if 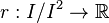 is a linear map, then
is a linear map, then 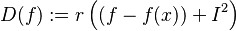 defines a derivation at
defines a derivation at  . This yields an equivalence between tangent spaces defined via derivations and tangent spaces defined via cotangent spaces.
. This yields an equivalence between tangent spaces defined via derivations and tangent spaces defined via cotangent spaces.
Properties
If 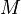 is an open subset of
is an open subset of 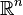 , then
, then 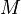 is a
is a 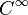 manifold in a natural manner (take coordinate charts to be identity maps on open subsets of
manifold in a natural manner (take coordinate charts to be identity maps on open subsets of 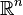 ), and the tangent spaces are all naturally identified with
), and the tangent spaces are all naturally identified with 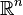 .
.
Tangent vectors as directional derivatives
Another way to think about tangent vectors is as directional derivatives. Given a vector 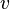 in
in 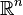 , one defines the corresponding directional derivative at a point
, one defines the corresponding directional derivative at a point 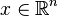 by
by
This map is naturally a derivation at  . Furthermore, every derivation at a point in
. Furthermore, every derivation at a point in 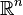 is of this form. Hence, there is a one-to-one correspondence between vectors (thought of as tangent vectors at a point) and derivations at a point.
is of this form. Hence, there is a one-to-one correspondence between vectors (thought of as tangent vectors at a point) and derivations at a point.
As tangent vectors to a general manifold at a point can be defined as derivations at that point, it is natural to think of them as directional derivatives. Specifically, if 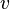 is a tangent vector to
is a tangent vector to 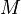 at a point
at a point  (thought of as a derivation), then define the directional derivative
(thought of as a derivation), then define the directional derivative 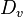 in the direction
in the direction 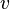 by
by
If we think of 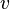 as the initial velocity of a differentiable curve
as the initial velocity of a differentiable curve 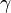 initialized at
initialized at  , i.e.,
, i.e., 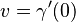 , then instead, define
, then instead, define 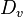 by
by
Basis of the tangent space at a point
For a 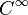 manifold
manifold 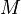 , if a chart
, if a chart 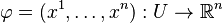 is given with
is given with 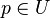 , then one can define an ordered basis
, then one can define an ordered basis 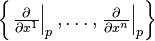 of
of 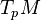 by
by
Then for every tangent vector 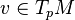 , one has
, one has
This formula therefore expresses 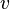 as a linear combination of the basis tangent vectors
as a linear combination of the basis tangent vectors  defined by the coordinate chart
defined by the coordinate chart 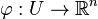 .
.
The derivative of a map
Every smooth (or differentiable) map  between smooth (or differentiable) manifolds induces natural linear maps between their corresponding tangent spaces:
between smooth (or differentiable) manifolds induces natural linear maps between their corresponding tangent spaces:
If the tangent space is defined via differentiable curves, then this map is defined by
If, instead, the tangent space is defined via derivations, then this map is defined by
The linear map 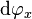 is called variously the derivative, total derivative, differential, or pushforward of
is called variously the derivative, total derivative, differential, or pushforward of 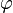 at
at  . It is frequently expressed using a variety of other notations:
. It is frequently expressed using a variety of other notations:
In a sense, the derivative is the best linear approximation to 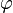 near
near  . Note that when
. Note that when  , then the map
, then the map 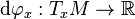 coincides with the usual notion of the differential of the function
coincides with the usual notion of the differential of the function 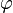 . In local coordinates the derivative of
. In local coordinates the derivative of 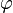 is given by the Jacobian.
is given by the Jacobian.
An important result regarding the derivative map is the following:
Theorem — If  is a local diffeomorphism at
is a local diffeomorphism at  in
in 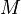 , then
, then 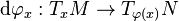 is a linear isomorphism. Conversely, if
is a linear isomorphism. Conversely, if  is continuously differentiable and
is continuously differentiable and 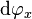 is an isomorphism, then there is an open neighborhood
is an isomorphism, then there is an open neighborhood  of
of  such that
such that  maps
maps  diffeomorphically onto its image.
diffeomorphically onto its image.
This is a generalization of the inverse function theorem to maps between manifolds.
See also
 In Spanish: Espacio tangente para niños
In Spanish: Espacio tangente para niños
- Coordinate-induced basis
- Cotangent space
- Differential geometry of curves
- Exponential map
- Vector space


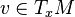 , along a curve traveling through
, along a curve traveling through ![\forall f \in {C^{\infty}}(\mathbb{R}^{n}): \qquad
(D_{v} f)(x) :=
\left. \frac{\mathrm{d}}{\mathrm{d}{t}} [f(x + t v)] \right|_{t = 0}
= \sum_{i = 1}^{n} v^{i} {\frac{\partial f}{\partial x^{i}}}(x).](/images/math/9/0/d/90d2992b5b99a5ee1325d12e74c52f90.png)

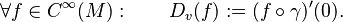
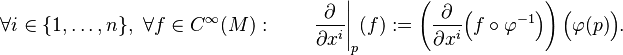
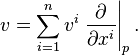
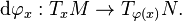
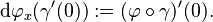
 := D(f \circ \varphi).](/images/math/5/5/8/55849c352352c6fe4c44e9f91e43c150.png)