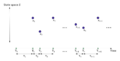Poisson point process facts for kids
A Poisson process is a stochastic process. It counts the number of occurrences of an event leading up to a specified time. This is a counting process where the increments of time are independent of one another (the times do not overlap).
Definition
The counting process known as the Poisson process is defined as:
- N(0) = 0.
- N(t) has independent increments.
- The number of arrivals in any interval of length 𝜏 > 0 follows a Poisson distribution.
Where N(t) is the total number of events that occur by time t.
Images for kids
-
According to one statistical study, the positions of cellular or mobile phone base stations in the Australian city Sydney, pictured above, resemble a realization of a homogeneous Poisson point process, while in many other cities around the world they do not and other point processes are required.
-
An illustration of a marked point process, where the unmarked point process is defined on the positive real line, which often represents time. The random marks take on values in the state space S known as the mark space. Any such marked point process can be interpreted as an unmarked point process on the space [0,\infty]\times S . The marking theorem says that if the original unmarked point process is a Poisson point process and the marks are stochastically independent, then the marked point process is also a Poisson point process on [0,\infty]\times S . If the Poisson point process is homogeneous, then the gaps \tau_i in the diagram are drawn from an exponential distribution.
See also
 In Spanish: Proceso de Poisson para niños
In Spanish: Proceso de Poisson para niños