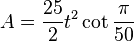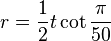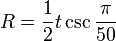Pentacontagon facts for kids
Quick facts for kids Regular pentacontagon |
|
|---|---|

A regular pentacontagon
|
|
| Type | Regular polygon |
| Edges and vertices | 50 |
| Schläfli symbol | {50}, t{25} |
| Coxeter diagram | |
| Symmetry group | Dihedral (D50), order 2×50 |
| Internal angle (degrees) | 172.8° |
| Dual polygon | Self |
| Properties | Convex, cyclic, equilateral, isogonal, isotoxal |
In geometry, a pentacontagon or pentecontagon or 50-gon is a fifty-sided polygon. The sum of any pentacontagon's interior angles is 8640 degrees.
Regular pentacontagon
A regular pentacontagon is represented by Schläfli symbol {50} and can be constructed as a quasiregular truncated icosipentagon, t{25}, which alternates two types of edges.
Area
One interior angle in a regular pentacontagon is 1724⁄5°, meaning that one exterior angle would be 71⁄5°.
The area of a regular pentacontagon is (with t = edge length)
and its inradius is
The circumradius of a regular pentacontagon is
Since 50 = 2 × 52, a regular pentacontagon is not constructible using a compass and straightedge, and is not constructible even if the use of an angle trisector is allowed.
Dissection
Coxeter states that every zonogon (a 2m-gon whose opposite sides are parallel and of equal length) can be dissected into m(m-1)/2 parallelograms. In particular this is true for regular polygons with evenly many sides, in which case the parallelograms are all rhombi. For the regular pentacontagon, m=25, it can be divided into 300: 12 sets of 25 rhombs. This decomposition is based on a Petrie polygon projection of a 25-cube.
 |
 |
 |
 |
- Eric W. Weisstein, Pentacontagon at MathWorld.
Images for kids
See also
 In Spanish: Pentacontágono para niños
In Spanish: Pentacontágono para niños