Norm (mathematics) facts for kids
In mathematics, the norm of a vector is its length. A vector is a mathematical object that has a size, called the magnitude, and a direction. For the real numbers, the only norm is the absolute value. For spaces with more dimensions, the norm can be any function 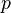 with the following three properties:
with the following three properties:
- Scales for real numbers
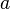 , that is,
, that is,  .
. - Function of sum is less than sum of functions, that is,
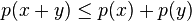 (also known as the triangle inequality).
(also known as the triangle inequality). 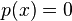 if and only if
if and only if  .
.
Contents
Definition
For a vector  , the associated norm is written as
, the associated norm is written as 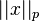 , or L
, or L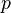 where
where 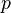 is some value. The value of the norm of
is some value. The value of the norm of  with some length
with some length 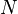 is as follows:
is as follows:
![||x||_p = \sqrt[p]{x_1^p+x_2^p+...+x_N^p}](/images/math/7/3/c/73c83a3f8df38938eac5dbf7a3b35910.png)
The most common usage of this is the Euclidean norm, also called the standard distance formula.
Examples
- The one-norm is the sum of absolute values:
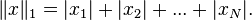 This is like finding the distance from one place on a grid to another by summing together the distances in all directions the grid goes; see Manhattan Distance.
This is like finding the distance from one place on a grid to another by summing together the distances in all directions the grid goes; see Manhattan Distance. - Euclidean norm (also called L2-norm) is the sum of the squares of the values:
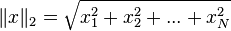
- Maximum norm is the maximum absolute value:
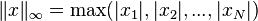
- When applied to matrices, the Euclidean norm is referred to as the Frobenius norm.
- L0 norm is the number of non-zero elements present in a vector.
Related pages
See also
 In Spanish: Norma vectorial para niños
In Spanish: Norma vectorial para niños

All content from Kiddle encyclopedia articles (including the article images and facts) can be freely used under Attribution-ShareAlike license, unless stated otherwise. Cite this article:
Norm (mathematics) Facts for Kids. Kiddle Encyclopedia.
