Molar heat capacity facts for kids

The molar heat capacity of a substance is the energy needed to raise the temperature of one mole of it by one degree Celsius.

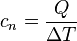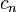When using SI units, it can be calculated with the equation where refers to the molar heat capcity (in joules per Kelvin), 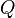to the heat supplied (in joules) and (in Kelvin) to the temperature change in the substance.

The molar heat capacity of a given substance can be found by heating the substance by releasing a known amount of energy into the substance and measuring the temperature change.

For example, a common school experiment to find the molar heat capacity of water involves heating a beaker of water with an immersion heater (that can display the heat released in joules on a display) and stirring the water, while checking the temperature at specific intervals.

For more accurate results, a bomb calorimeter can be used; these contain a chamber of fuel (in this case, a compound that will release heat when needed) inside a chamber of water, with the water chamber protected by heat-proof walls (to ensure minimal heat loss, which would affect the final heat capacity recorded).

Images for kids

• 

  Vibrations of atoms in a molecule consume some of the heat energy that otherwise would contribute to the molecule's kinetic energy.

• 

  Constant-volume specific heat capacity of a diatomic gas (idealised). As temperature increases, heat capacity goes from 3/2R (translation contribution only), to 5/2R (translation plus rotation), finally to a maximum of 7/2R (translation + rotation + vibration)

• 

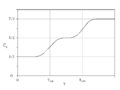
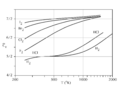
  Constant-volume specific heat capacity of diatomic gases (real gases) between about 200 K and 2000 K. This temperature range is not large enough to include both quantum transitions in all gases. Instead, at 200 K, all but hydrogen are fully rotationally excited, so all have at least 5/2R heat capacity. (Hydrogen is already below 5/2, but it will require cryogenic conditions for even H2 to fall to 3/2R). Further, only the heavier gases fully reach 7/2R at the highest temperature, due to the relatively small vibrational energy spacing of these molecules. HCl and H2 begin to make the transition above 500 K, but have not achieved it by 1000 K, since their vibrational energy level spacing is too wide to fully participate in heat capacity, even at this temperature.

• 

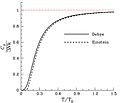
  The dimensionless heat capacity divided by three, as a function of temperature as predicted by the Debye model and by Einstein's earlier model. The horizontal axis is the temperature divided by the Debye temperature. Note that, as expected, the dimensionless heat capacity is zero at absolute zero, and rises to a value of three as the temperature becomes much larger than the Debye temperature. The red line corresponds to the classical limit of the Dulong–Petit law