Method of moments (statistics) facts for kids
In statistics, the method of moments is a method of estimation of population parameters.
Method
Suppose that the problem is to estimate 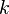 unknown parameters
unknown parameters 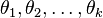 describing the distribution
describing the distribution 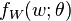 of the random variable
of the random variable 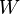 . Suppose the first
. Suppose the first 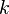 moments of the true distribution (the "population moments") can be expressed as functions of the
moments of the true distribution (the "population moments") can be expressed as functions of the 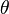 s:
s:
Suppose a sample of size 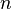 is drawn, and it leads to the values
is drawn, and it leads to the values 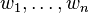 . For
. For 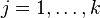 , let
, let
be the j-th sample moment, an estimate of 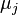 . The method of moments estimator for
. The method of moments estimator for  denoted by
denoted by 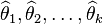 is defined as the solution (if there is one) to the equations:
is defined as the solution (if there is one) to the equations:
Reasons to use it
The method of moments is simple and gets consistent estimators (under very weak assumptions). However, these estimators are often biased.
See also
 In Spanish: Método de momentos (estadística) para niños
In Spanish: Método de momentos (estadística) para niños

All content from Kiddle encyclopedia articles (including the article images and facts) can be freely used under Attribution-ShareAlike license, unless stated otherwise. Cite this article:
Method of moments (statistics) Facts for Kids. Kiddle Encyclopedia.

![\begin{align}
\mu_1 & \equiv \operatorname E[W]=g_1(\theta_1, \theta_2, \ldots, \theta_k) , \\[4pt]
\mu_2 & \equiv \operatorname E[W^2]=g_2(\theta_1, \theta_2, \ldots, \theta_k), \\
& \,\,\, \vdots \\
\mu_k & \equiv \operatorname E[W^k]=g_k(\theta_1, \theta_2, \ldots, \theta_k).
\end{align}](/images/math/e/a/e/eaea0e283767b8b1200be0c5008af05e.png)
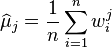
![\begin{align}
\widehat \mu_1 & = g_1(\widehat\theta_1, \widehat\theta_2, \ldots, \widehat\theta_k), \\[4pt]
\widehat \mu_2 & = g_2(\widehat\theta_1, \widehat\theta_2, \ldots, \widehat\theta_k), \\
& \,\,\, \vdots \\
\widehat \mu_k & = g_k(\widehat\theta_1, \widehat\theta_2, \ldots, \widehat\theta_k).
\end{align}](/images/math/e/3/7/e37b98210f2925a542238c1f22793b0a.png)