In the study of orbital dynamics the mean anomaly of an orbiting body is the angle the body would have traveled about the center of the orbit's auxiliary circle. Unlike other measures of anomaly, the mean anomaly grows linearly with time. Because of the linear growth with time, the mean anomaly makes calculating the time of flight between two points on the orbit very easy. The mean anomalies for the two points are calculated and their difference is found. Knowing this, the ratio of this difference relative to the entire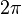 
encompassing one orbit is simply equal to ratio of the time of flight to the orbital period of one whole orbit (i.e. 
).
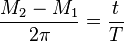Images for kids
-
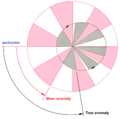
Area swept out per unit time by an object in an elliptical orbit, and by an imaginary object in a circular orbit (with the same orbital period). Both sweep out equal areas in equal times, but the angular rate of sweep varies for the elliptical orbit and is constant for the circular orbit. Shown are mean anomaly and true anomaly for two units of time. (Note that for visual simplicity, a non-overlapping circular orbit is diagrammed, thus this circular orbit with same orbital period is not shown in true scale with this elliptical orbit: for scale to be true for the two orbits of equal period, these orbits must intersect.)
See also
In Spanish: Anomalía media para niños
