Luminosity facts for kids
Luminosity is an absolute measure of radiated electromagnetic energy per unit time, and is synonymous with the radiant power emitted by a light-emitting object. In astronomy, luminosity is the total amount of electromagnetic energy emitted per unit of time by a star, galaxy, or other astronomical objects.
In SI units, luminosity is measured in joules per second, or watts. In astronomy, values for luminosity are often given in the terms of the luminosity of the Sun, L⊙. Luminosity can also be given in terms of the astronomical magnitude system: the absolute bolometric magnitude (Mbol) of an object is a logarithmic measure of its total energy emission rate, while absolute magnitude is a logarithmic measure of the luminosity within some specific wavelength range or filter band.
In contrast, the term brightness in astronomy is generally used to refer to an object's apparent brightness: that is, how bright an object appears to an observer. Apparent brightness depends on both the luminosity of the object and the distance between the object and observer, and also on any absorption of light along the path from object to observer. Apparent magnitude is a logarithmic measure of apparent brightness. The distance determined by luminosity measures can be somewhat ambiguous, and is thus sometimes called the luminosity distance.
Measurement
When not qualified, the term "luminosity" means bolometric luminosity, which is measured either in the SI units, watts, or in terms of solar luminosities (L☉). A bolometer is the instrument used to measure radiant energy over a wide band by absorption and measurement of heating. A star also radiates neutrinos, which carry off some energy (about 2% in the case of the Sun), contributing to the star's total luminosity. The IAU has defined a nominal solar luminosity of 3.828×1026 W to promote publication of consistent and comparable values in units of the solar luminosity.
While bolometers do exist, they cannot be used to measure even the apparent brightness of a star because they are insufficiently sensitive across the electromagnetic spectrum and because most wavelengths do not reach the surface of the Earth. In practice bolometric magnitudes are measured by taking measurements at certain wavelengths and constructing a model of the total spectrum that is most likely to match those measurements. In some cases, the process of estimation is extreme, with luminosities being calculated when less than 1% of the energy output is observed, for example with a hot Wolf-Rayet star observed only in the infrared. Bolometric luminosities can also be calculated using a bolometric correction to a luminosity in a particular passband.
The term luminosity is also used in relation to particular passbands such as a visual luminosity of K-band luminosity. These are not generally luminosities in the strict sense of an absolute measure of radiated power, but absolute magnitudes defined for a given filter in a photometric system. Several different photometric systems exist. Some such as the UBV or Johnson system are defined against photometric standard stars, while others such as the AB system are defined in terms of a spectral flux density.
Luminosity formulae
The Stefan–Boltzmann equation applied to a black body gives the value for luminosity for a black body, an idealized object which is perfectly opaque and non-reflecting: 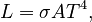 where A is the surface area, T is the temperature (in kelvins) and σ is the Stefan–Boltzmann constant, with a value of 5.670374419...×10−8 W⋅m−2⋅K−4.
where A is the surface area, T is the temperature (in kelvins) and σ is the Stefan–Boltzmann constant, with a value of 5.670374419...×10−8 W⋅m−2⋅K−4.
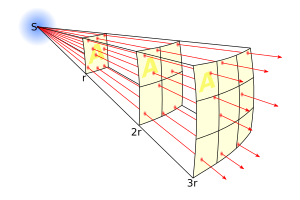
Imagine a point source of light of luminosity 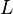 that radiates equally in all directions. A hollow sphere centered on the point would have its entire interior surface illuminated. As the radius increases, the surface area will also increase, and the constant luminosity has more surface area to illuminate, leading to a decrease in observed brightness.
that radiates equally in all directions. A hollow sphere centered on the point would have its entire interior surface illuminated. As the radius increases, the surface area will also increase, and the constant luminosity has more surface area to illuminate, leading to a decrease in observed brightness.
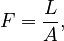 where
where
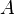 is the area of the illuminated surface.
is the area of the illuminated surface.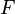 is the flux density of the illuminated surface.
is the flux density of the illuminated surface.
The surface area of a sphere with radius r is  , so for stars and other point sources of light:
, so for stars and other point sources of light: 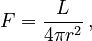 where
where  is the distance from the observer to the light source.
is the distance from the observer to the light source.
For stars on the main sequence, luminosity is also related to mass approximately as below: 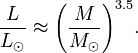
Relationship to magnitude
Luminosity is an intrinsic measurable property of a star independent of distance. The concept of magnitude, on the other hand, incorporates distance. The apparent magnitude is a measure of the diminishing flux of light as a result of distance according to the inverse-square law. The Pogson logarithmic scale is used to measure both apparent and absolute magnitudes, the latter corresponding to the brightness of a star or other celestial body as seen if it would be located at an interstellar distance of 10 parsecs (3.1×1017 metres). In addition to this brightness decrease from increased distance, there is an extra decrease of brightness due to extinction from intervening interstellar dust.
By measuring the width of certain absorption lines in the stellar spectrum, it is often possible to assign a certain luminosity class to a star without knowing its distance. Thus a fair measure of its absolute magnitude can be determined without knowing its distance nor the interstellar extinction.
In measuring star brightnesses, absolute magnitude, apparent magnitude, and distance are interrelated parameters—if two are known, the third can be determined. Since the Sun's luminosity is the standard, comparing these parameters with the Sun's apparent magnitude and distance is the easiest way to remember how to convert between them, although officially, zero point values are defined by the IAU.
The magnitude of a star, a unitless measure, is a logarithmic scale of observed visible brightness. The apparent magnitude is the observed visible brightness from Earth which depends on the distance of the object. The absolute magnitude is the apparent magnitude at a distance of 10 pc (3.1×1017 m), therefore the bolometric absolute magnitude is a logarithmic measure of the bolometric luminosity.
The difference in bolometric magnitude between two objects is related to their luminosity ratio according to: 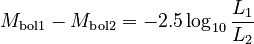
where:
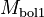 is the bolometric magnitude of the first object
is the bolometric magnitude of the first object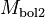 is the bolometric magnitude of the second object.
is the bolometric magnitude of the second object.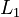 is the first object's bolometric luminosity
is the first object's bolometric luminosity is the second object's bolometric luminosity
is the second object's bolometric luminosity
The zero point of the absolute magnitude scale is actually defined as a fixed luminosity of 3.0128×1028 W. Therefore, the absolute magnitude can be calculated from a luminosity in watts:  where L0 is the zero point luminosity 3.0128×1028 W
where L0 is the zero point luminosity 3.0128×1028 W
and the luminosity in watts can be calculated from an absolute magnitude (although absolute magnitudes are often not measured relative to an absolute flux): 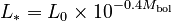
Images for kids
-
The Sun has an intrinsic luminosity of 3.83×1026 watts. In astronomy, this amount is equal to one solar luminosity, represented by the symbol L⊙. A star with four times the radiative power of the sun has a luminosity of 4 L⊙.
See also
 In Spanish: Luminosidad para niños
In Spanish: Luminosidad para niños