Louis Bachelier facts for kids
Quick facts for kids
Louis Bachelier
|
|
|---|---|
 |
|
| Born | 11 March 1870 Le Havre, France
|
| Died | 28 April 1946 (aged 76) Saint-Servan-sur-Mer, France
|
| Nationality | French |
| Alma mater | University of Paris |
| Known for | Pioneer in mathematical finance |
| Scientific career | |
| Fields | Mathematics |
| Institutions | University of Paris Université de Franche-Comté (Besançon) Université de Dijon University of Rennes |
| Thesis | Théorie de la spéculation (The Theory of Speculation) (1900) |
| Doctoral advisor | Henri Poincaré |
Louis Jean-Baptiste Alphonse Bachelier (French: [baʃəlje]; 11 March 1870 – 28 April 1946) was a French mathematician at the turn of the 20th century. He is credited with being the first person to model the stochastic process now called Brownian motion, as part of his doctoral thesis The Theory of Speculation (Théorie de la spéculation, defended in 1900).
Bachelier's doctoral thesis, which introduced the first mathematical model of Brownian motion and its use for valuing stock options, was the first paper to use advanced mathematics in the study of finance. His Bachelier model has been influential in the development of other widely used models, including the Black-Scholes model.
Bachelier is considered as the forefather of mathematical finance and a pioneer in the study of stochastic processes.
Early years
Bachelier was born in Le Havre, in Seine-Maritime. His father was a wine merchant and amateur scientist, and the vice-consul of Venezuela at Le Havre. His mother was the daughter of an important banker (who was also a writer of poetry books). Both of Louis's parents died just after he completed his high school diploma ("baccalauréat" in French), forcing him to take care of his sister and three-year-old brother and to assume the family business, which effectively put his graduate studies on hold. During this time Bachelier gained a practical acquaintance with the financial markets. His studies were further delayed by military service. Bachelier arrived in Paris in 1892 to study at the Sorbonne, where his grades were less than ideal.
The doctoral thesis
Defended on 29 March 1900 at the University of Paris, Bachelier's thesis was not well received because it attempted to apply mathematics to an area mathematicians found unfamiliar. However, his instructor, Henri Poincaré, is recorded as having given some positive feedback (though insufficient to secure Bachelier an immediate teaching position in France at that time). For example, Poincaré called his approach to deriving Gauss's law of errors
very original, and all the more interesting in that Fourier's reasoning can be extended with a few changes to the theory of errors. ... It is regrettable that M. Bachelier did not develop this part of his thesis further.
The thesis received a grade of honorable, and was accepted for publication in the prestigious Annales Scientifiques de l’École Normale Supérieure. While it did not receive a mark of très honorable, despite its ultimate importance, the grade assigned is still interpreted as an appreciation for his contribution. Jean-Michel Courtault et al. point out in "On the Centenary of Théorie de la spéculation" that honorable was "the highest note which could be awarded for a thesis that was essentially outside mathematics and that had a number of arguments far from being rigorous."
Academic career
For several years following the successful defense of his thesis, Bachelier further developed the theory of diffusion processes, and was published in prestigious journals. In 1909 he became a "free professor" at the Sorbonne. In 1914, he published a book, Le Jeu, la Chance, et le Hasard (Games, Chance, and Randomness), that sold over six thousand copies. With the support of the Council of the University of Paris, Bachelier was given a permanent professorship at the Sorbonne, but World War I intervened and he was drafted into the French army as a private. His army service ended on December 31, 1918. In 1919, he found a position as an assistant professor in Besançon, replacing a regular professor on leave. He married Augustine Jeanne Maillot in September 1920 but was soon widowed. When the professor returned in 1922, Bachelier replaced another professor at Dijon. He moved to Rennes in 1925, but was finally awarded a permanent professorship in 1927 at the University of Besançon, where he worked for 10 years until his retirement.
Besides the setback that the war had caused him, Bachelier was blackballed in 1926 when he attempted to receive a permanent position at Dijon. This was due to a "misinterpretation" of one of Bachelier's papers by Professor Paul Lévy, who—to Bachelier's understandable fury—knew nothing of Bachelier's work, nor of the candidate that Lévy recommended above him. Lévy later learned of his error, and reconciled himself with Bachelier.
Although Bachelier's work on random walks predated Einstein's celebrated study of Brownian motion by five years, the pioneering nature of his work was recognized only after several decades, first by Andrey Kolmogorov who pointed out his work to Paul Lévy, then by Leonard Jimmie Savage who translated Bachelier's thesis into English and brought the work of Bachelier to the attention of Paul Samuelson. The arguments Bachelier used in his thesis also predate Eugene Fama's efficient-market hypothesis, which is very closely related, as the idea of a random walk is suited to predict the random future in a stock market where everyone has all the available information. His work in finance is recognized as one of the foundations for the Black–Scholes model.
Works
- , Théorie de la spéculation
- Also published as a book,
- Republished in a book of combined works,
- Translated into English,
- Translated into English with additional commentary and background,
- Translated into English,
- , Théorie mathématique du jeu
- Republished in a book of combined works,
- , Théorie des probabilités continues
- , Étude sur les probabilités des causes
- , Le problème général des probabilités dans les épreuves répétées
- , Les probabilités à plusieurs variables
- , Mouvement d’un point ou d’un système matériel soumis à l’action de forces dépendant du hasard
- , (Book) Calcul des probabilités
- Republished,
- , Les probabilités cinématiques et dynamiques
- , Les probabilités semi-uniformes
- , (Book) Le Jeu, la Chance et le Hasard
- Republished,
- Translated into English, Harding 2017
- , La périodicité du hasard
- , Sur la théorie des corrélations
- , Sur les décimales du nombre
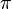
- , Le problème général de la statistique discontinue
- , Quelques curiosités paradoxales du calcul des probabilités
- , (Book) Les lois des grands nombres du Calcul des Probabilités (Book)
- , (Book) La spéculation et le Calcul des Probabilités
- , (Book) Les nouvelles méthodes du Calcul des Probabilités
- , Probabilités des oscillations maxima
- Erratum,
See also
 In Spanish: Louis Bachelier para niños
In Spanish: Louis Bachelier para niños
- Black–Scholes equation
- Bachelier model
- Martingale
- Random walk
- Brownian Motion
- Louis Bachelier Prize
- Henri Poincaré
- Vinzenz Bronzin
- Jules Regnault

