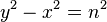Lorentz transformation facts for kids

Kids Encyclopedia Facts

The Lorentz transformations is a set of equations that describe a linear transformation between a stationary reference frame and a reference frame in constant velocity. The equations are given by:

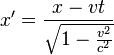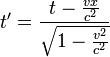
$x'=\frac{x-vt}{\sqrt{1-\frac{v^2}{c^2}}}$ , $y'=y$ , $z'=z$ , $t'=\frac{t-\frac{vx}{c^2}}{\sqrt{1-\frac{v^2}{c^2}}}$

where 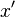$x'$ represents the new x co-ordinate, 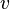$v$ represents the velocity of the other reference frame, $t$ representing time, and $c$ the speed of light.

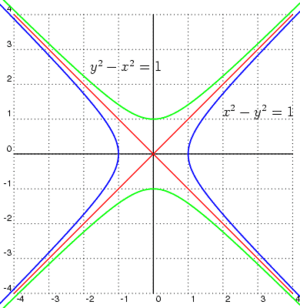
On a Cartesian coordinate system, with the vertical axis being time (t), the horizontal axis being position in space along one axis (x), the gradients represent velocity (shallower gradient resulting in a greater velocity). If the speed of light is set as a 45° or 1:1 gradient, Lorentz transformations can rotate and squeeze other gradients while keeping certain gradients, like a 1:1 gradient constant. Points undergoing a Lorentz transformations on such a plane will be transformed along lines corresponding to 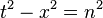$t^2-x^2=n^2$ where n is some number

Points undergoing a Lorentz transformation follow the green, conjugate hyperbola, where the vertical axis represents time,

y^2-x^2=n^2

Lorentz transformation facts for kids

See also