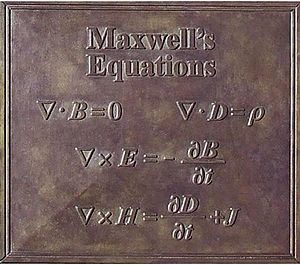James Clerk Maxwell Foundation facts for kids
The James Clerk Maxwell Foundation is a registered Scottish charity set up in 1977. By supporting physics and mathematics, it honors one of the greatest physicists, James Clerk Maxwell (1831–1879), and while attempting to increase the public awareness and trust of science. It maintains a small museum in Maxwell's birthplace. This museum is owned by the Foundation.
Purpose

The James Clerk Maxwell Foundation aims to increase the public awareness of the many scientific advances made by Maxwell over his lifetime and to highlight their importance in the world today. It summarizes Maxwell's many innovative technical advances and displays, in Maxwell’s birthplace, the history of Maxwell's family. The Foundation awards grants and prizes and supports mathematical challenges designed to encourage young students to study as mathematicians, scientists and engineers and become leaders in the world.
History
The James Clerk Maxwell Foundation was formed in 1977 by the late Sydney Ross, Professor of Colloidal chemistry at Rensselaer Polytechnic Institute in New York, USA. Ross was born in Scotland and he inherited monies from his late father’s whisky business, Ross, Campbell Ltd.
In 1993, the Foundation acquired 14 India Street, Edinburgh, the birthplace of Maxwell.
Since 1993, the house has been refurbished to its original standard and a small museum has been developed which features Maxwell’s family, life and scientific advances. These have resulted in Maxwell now being recognised as the most famous scientist in the era between Newton and Einstein.
Maxwell's birthplace
Maxwell was born at 14 India Street on 13 June 1831. This four-floor townhouse has 3–4 rooms on each floor. The Foundation lets the basement and top floor to tenants and maintains on the ground and first floor a modest museum which can be opened for visits by prior appointment.
Maxwell’s father, John Clerk Maxwell of Middlebie, had previously inherited land at Corsock in Galloway and he divided his time between Galloway and his 1820s townhouse in Edinburgh’s New Town. In 1830, John Clerk Maxwell commenced building a new house on his Corsock farm and would later name this Glenlair House. The Clerk Maxwell family moved permanently to Glenlair when James was two years old. Maxwell’s mother died when he was only eight years old and, two years later, he returned to Edinburgh to attend school at the Edinburgh Academy.
Maxwell studied at the University of Edinburgh and the University of Cambridge and his career followed professorial appointments at Marischal College Aberdeen, King's College London and the University of Cambridge. While in Aberdeen, Maxwell married the College Principal’s daughter Katherine Dewar.
Museum
The restored entrance hall contains a copy of the bust of Maxwell by Charles d’Orville Pilkington Jackson, the original is located at Marischal College, Aberdeen. The Milestone in Electrical Engineering and Computing plaque by the American Institute of Electrical and Electronics Engineers (IEEE) commemorates Maxwell’s contributions to electromagnetic theory. Displayed here is a timeline starting with Maxwell’s life and going up to today, where Maxwell’s electromagnetics is central to the performance of cellular mobile phones, GPS and Radar.
Exhibition Room
This room, originally the dining room, contains several family portraits: a copy of James Clerk Maxwell by Lowes Cato Dickinson located in Trinity College, Cambridge; and of Maxwell’s father, John Clerk Maxwell. Early pastels from the Cay’s, his mother’s family, of Maxwell’s uncles, Robert and John, his aunt Jane and Maxwell’s mother Frances Cay. These are by Maxwell’s maternal grandmother, Elizabeth Cay, there is also a portrait in oils, after Sir Henry Raeburn, of Elizabeth’s husband Robert Hodshon Cay by Maxwell's cousin, Isabella Cay (1850–1934). The final portrait is of Maxwell’s lifelong friend and scientific colleague Peter Guthrie Tait who was the Professor of Natural Philosophy at Edinburgh University.
One of Maxwell’s major technical advances is the first full colour projected image produced at a time when only black-and-white photography was known. The projection of this coloured image on a screen was famously demonstrated in 1861 at Faraday's Royal Institution in London. In this, the foundation of virtually all practical colour processes, he made three black-and-white photographic plates which were photographed through red, green and blue filters respectively. He then used three magic lanterns to superimpose these three black-and-white images, each projected through the same red, green and blue filters, to produce the first colour image of the ‘tartan ribbon’. This production of colour images is still used today in printing, digital cameras, televisions, and computers.
The replica of Maxwell’s colour box, which he used to quantitatively analyse and synthesise light colours in order to underpin his observations on colour mixing and colour perception (thereby extending Newton's work on Optics), was produced in the Cavendish Laboratory, Cambridge University.
Maxwell’s most celebrated contribution was in deriving the equations governing electromagnetics (Maxwell’s equations). In his 1865 paper, A Dynamical Theory of the Electromagnetic Field, Maxwell defined electromagnetics in terms of 20 equations, later summarised in his 1873 book Treatise on Electricity and Magnetism. Hendrik Lorentz subsequently reinterpreted these as the fundamental equations of electrodynamics and Oliver Heaviside developed the notation we use today.
The theory behind Maxwell's equations was the first grand unification theory of the forces of Nature as this theory united the electric and magnetic fields. A person who is stationary may experience only an electric field but a person who is in relative motion may experience an electric current and a magnetic field. Thus the one field (called the electromagnetic field) may appear in different guises.
In his famous 1905 'Special Relativity' paper, Albert Einstein showed that Maxwell's equations were invariant under a Lorentz transformation (as opposed to a Galilean transformation) and, inter alia, used this evidence to support his 'relativity theory' that the Lorentz transformation was the true transformation of Nature (between the viewpoints of two observers, one moving at a constant speed and direction relative to each other).
On display is a replica of part of the balance arm of Maxwell’s apparatus to measure the ratio of electromagnetic to electrostatic units of electrical charge. Maxwell showed mathematically that the numerical value of this ratio was equal to the speed of electromagnetic waves. Maxwell recognised that the speed of electromagnetic waves (as derived from his equations) was also equal to the speed of light as measured by Fizeau and as previously measured in the 17th century by Ole Roemer. In his 1865 paper, Maxwell stated the immortal words “…it seems we have strong reason to conclude that light itself (including radiant heat and other radiations if any) is an electromagnetic disturbance in the form of waves propagated …according the electromagnetic laws”. This was stated by the Nobel Laureate physicist Richard Feynman in 1964 to be the most stunning conclusion of 19th-century theoretical physics!
The display cabinet shows a few pages, on loan from The Edinburgh Academy, of Maxwell’s work on oval curves, where Maxwell simplified earlier work of René Descartes. He presented this work to the Royal Society of Edinburgh (or rather Professor Forbes did as Maxwell, then aged 14, was considered too young!). Maxwell's second scientific paper "The Theory of Rolling Curves" was written at age 17 while at university in Edinburgh. The cabinet displays here 3 of Maxwell's medals: the 1860 Rumford Medal from Royal Society for colour composition, the 1871 Keith Medal from Royal Society of Edinburgh for forces and frames in structures, and the 1878 Volta Medal from University of Pavia, when he was awarded an honorary degree.
The Library
This room (originally John Clerk Maxwell's business office when he practised as an advocate in Edinburgh) contains wall displays celebrating Maxwell’s other major scientific achievements: his work on governors for machine speed control; Maxwell–Boltzmann distribution and his contribution to statistical physics; discovery of the form of Saturn's rings; contributing to the committee that defined the Ohm; reciprocal figures or frames for the design of structures such roofs and bridges. The final set of wall panels describes the friezes on his Edinburgh statue placing Maxwell’s contributions in context between Newton and Einstein. The library also contains a selection of books on Maxwell, Newton, Lord Kelvin, Michael Faraday etc.
The Staircase
The engravings on the staircase walls are from Sir John Herschel's Collection purchased by our founder, Sydney Ross. They sample the history of science and mathematics from Copernicus onwards, arriving at Maxwell’s contemporaries Michael Faraday and Lord Kelvin.
Upper Exhibition Room
The upper exhibition room is the annexe of the original drawing room, and it was in this room that James Clerk Maxwell was born in 1831. It displays material relating to the Clerk family, Maxwell’s childhood, early life and career, including some of his poetry. There is a reproduction of the William Dyce portrait of James and his mother, from Birmingham art galleries (Dyce was the brother of Maxwell's aunt). The main display here is of watercolours by Maxwell’s cousin Jemima Wedderburn. Jemima later married Hugh Blackburn, Professor of Mathematics at Glasgow University and a colleague of Lord Kelvin.
Conference Room
The Conference Room, originally the Drawing Room, which is used for receptions and seminars contains a Latin epigram which can be translated as: "From this house of his birth, his name is now widespread – across the entire terrestrial globe and even to the stars". The major painting here (by Lady Lucinda L. Mackay) is of a near neighbour, Nobel Laureate and Honorary Patron of the Foundation, Professor Peter Higgs, whose research led to the search, in the Large Hadron Collider, to confirm the existence of the Higgs boson.