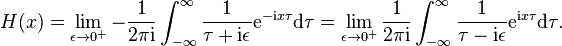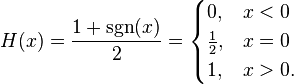Heaviside Function facts for kids
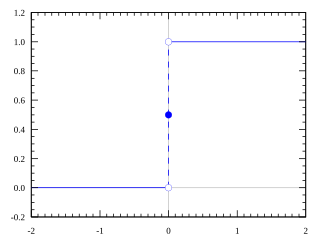
The Heaviside function, often written as H(x), is a non-continuous function whose value is zero for a negative input and one for a positive input.
The function is used in the mathematics of control theory to represent a signal that switches on at a specified time, and which stays switched on indefinitely. It was named after the Englishman Oliver Heaviside.
The Heaviside function is the integral of the Dirac delta function: H′(x) = δ(x). This is sometimes written as
Contents
Discrete form
We can also define an alternative form of the Heaviside step function as a function of a discrete variable n:
where n is an integer.
Or
The discrete-time unit impulse is the first difference of the discrete-time step
This function is the cumulative summation of the Kronecker delta:
where
is the discrete unit impulse function.
Representations
Often an integral representation of the Heaviside step function is useful:
H(0)
The value of the function at 0 can be defined as H(0) = 0, H(0) = ½ or H(0) = 1. In particular:
Related pages
- Laplace transform
- Step function


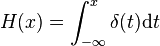
![H[n]=\begin{cases} 0, & n < 0 \\ 1, & n \ge 0 \end{cases}](/images/math/7/4/1/7410747ec7563eab51f608f2c80a9497.png)
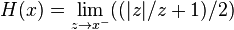
![\delta\left[ n \right] = H[n] - H[n-1].](/images/math/1/8/b/18b1fdb556783d82836628433d71fa6d.png)
![H[n] = \sum_{k=-\infty}^{n} \delta[k] \,](/images/math/8/a/c/8ac2212bc01e69e22245f783f82146fd.png)
![\delta[k] = \delta_{k,0} \,](/images/math/4/3/0/430fc704633ce64f5d7aa81d9d45df7c.png)