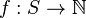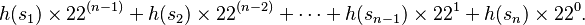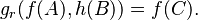Gödel number facts for kids
In formal number theory a Gödel numbering is a function which assigns to each symbol and formula of some formal language a unique natural number called a Gödel number (GN). The concept was first used by Kurt Gödel for the proof of his incompleteness theorem.
A Gödel numbering can be interpreted as an encoding where a number is assigned to each symbol of a mathematical notation, and a stream of natural numbers can then represent some form or function. A numbering of the set of computable functions can then be represented by a stream of Gödel numbers (also called effective numbers). Rogers' equivalence theorem states criteria for which those numberings of the set of computable functions are Gödel numberings.
Definition
Given a countable set S, a Gödel numbering is an injective function
with both f and 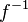 (the inverse of f) being computable functions.
(the inverse of f) being computable functions.
Examples
Base notation and strings
One of the simplest Gödel numbering schemes is used every day: The correspondence between integers and their representations as strings of symbols. For example, the sequence 2 3 is understood, by a particular set of rules, to correspond to the number twenty-three. Similarly, strings of symbols from some alphabet of N symbols can be encoded by identifying each symbol with a number from 0 to N and reading the string as the base N+1 representation of an integer.
encodes arbitrary sequences of any positive integers, which allowed Gödel to encode not just strings of symbols, but sequences of strings as well. Given a sequence 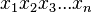 of positive integers, the Gödel encoding is the product of the first n primes raised to their corresponding values in the sequence:
of positive integers, the Gödel encoding is the product of the first n primes raised to their corresponding values in the sequence:
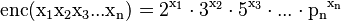
According to the fundamental theorem of arithmetic, any code obtained this way can be uniquely factored into prime factors, so it is possible to recover the original sequence. See also a more sophisticated (but more “concise”) way to construct Gödel numbering for sequences.
Gödel specifically used this scheme at two levels: first, to encode sequences of symbols representing formulas, and second, to encode sequences of formulas representing proofs. This allowed him to show a correspondence between statements about natural numbers and statements about the provability of theorems about natural numbers, the key observation of the proof.
Discussion
This Gödel numbering is not unique. The general idea is to map formulas onto natural numbers. An alternative Gödel numbering could be to consider each of the symbols of Step 1 to be mapped (through, say, a mapping h) to a digit of a base-22 numeral system, so a formula consisting of a string of n symbols 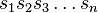 would be mapped to the number
would be mapped to the number
Also, Gödel numbering implies that each inference rule of the formal system can be expressed as a function of natural numbers. If f is the Gödel mapping and if formula C can be derived from formulas A and B through an inference rule r, i.e.
then there should be some arithmetical function gr of natural numbers such that
Then, since the formal system is a formal arithmetic, which can make statements about numbers and their arithmetical relationships to each other, it follows that the system can also, by means of Gödel coding, indirectly make statements about itself: that is, a proposition of the formal system can make assertions which, when viewed through the perspective of the Gödel mapping, translate into assertions about other propositions of the same formal system, or even about itself. Thus, by this means a formal arithmetic can make assertions about itself, becoming self-referential, almost like a second-order logic. This provided Gödel (and other logicians) with a means of exploring and discovering proofs about consistency and completeness properties of formal systems.
Related pages
- Church numeral
- Description number
- Gödel's incompleteness theorems
-->
- Gödel, Kurt, "Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme I", Monatsheft für Math. und Physik 38, 1931, pages 173–198.
- Gödel, Escher, Bach: an Eternal Golden Braid, by Douglas Hofstadter. This book defines and uses an alternative Gödel numbering.
- Gödel's Proof by Ernest Nagel and James R. Newman. This book provides a good introduction and summary of the proof, with a large section dedicated to Gödel's numbering.
See also
 In Spanish: Numeración de Gödel para niños
In Spanish: Numeración de Gödel para niños