Fundamental theorem of algebra facts for kids

The fundamental theorem of algebra is a proven fact about polynomials, sums of multiples of integer powers of one variable. It is based on mathematical analysis, the study of real numbers and limits. It was first proven by German mathematician Carl Friedrich Gauss. It says that for any polynomial 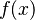$f(x)$ with the degree 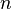$n$ , where 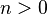$n>0$ , the polynomial equation 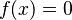$f(x)=0$ must have at least one root 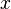$x$ , and not more than 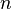$n$ roots altogether.

Some remarks:

the degree 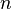$n$ of a polynomial is the highest power of 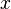$x$ that occurs in it
some of the roots may be complex numbers
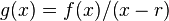it is possible to 'count' a root $r$ twice, if $r$ is still a root of the polynomial $g(x) = f(x)/(x-r)$ ; if you will 'count' the roots in this way, then the polynomial 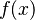$f(x)$ with degree 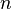$n$ has exactly 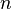$n$ roots
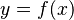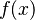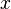it is not a theorem of pure algebra. It is not possible to prove this theorem without an element of analysis. This element has been reduced to the observation that, firstly, for polynomial functions $y=f(x)$ of odd degree the pair of values $f(x)$ and $f(-x)$ has opposite positive and negative signs when $x$ is large enough. And secondly, that any polynomial function 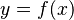$y=f(x)$ on the real line that takes positive and negative values for 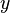$y$ has to cross 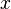$x$ axis.

See also