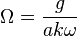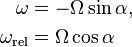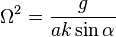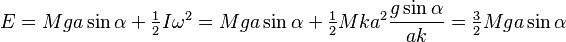Euler's Disk facts for kids
Euler's Disk, invented between 1987 and 1990 by Joseph Bendik, is a trademark for a scientific educational toy. It is used to illustrate and study the dynamical system of a spinning and rolling disk on a flat or curved surface, and it has been the subject of a number of scientific papers.
Contents
Discovery
Joseph Bendik first noted the interesting motion of the spinning disk while working at Hughes Aircraft (Carlsbad Research Center) after spinning a heavy polishing chuck on his desk at lunch one day. The spinning effect was so dramatic that he immediately called his friend and co-worker Richard Henry Wyles to take a look. He also called his friend Larry Shaw (Astrojax inventor) on the phone and had him listen to the sound of the spinning disk. For the next several years, Joe, Rich, and Larry worked to optimize the motion of the disk and develop a commercial version of the toy.
The apparatus is known as a dramatic visualization of energy exchanges in three different, tightly coupled processes. As the disk gradually decreases its azimuthal rotation, there is also a decrease in amplitude and increase in the frequency of the disk's axial precession.
The evolution of the disk's axial precession is easily visualized in a slow motion video by looking at the side of the disk following a single point marked on the disk. The evolution of the rotation of the disk is easily visualized in slow motion by looking at the top of the disk following an arrow drawn on the disk representing its radius.
As the disk releases the initial energy given by the user and approaches a halt, the disk seems to defy gravity through these dynamic exchanges of energy. Bendik named the toy after Leonhard Euler, who studied similar physics in the 18th century.
Components and operation
The commercially available toy consists of a heavy, thick chrome-plated steel disk and a rigid, slightly concave, mirrored base. Included holographic magnetic stickers can be attached to the disk, to enhance the visual effect of wobbling. These attachments are strictly decorative and may reduce the capacity to see and understand what processes are truly at work.
The disk, when spun on a flat surface, exhibits a spinning/rolling motion, slowly progressing through different rates and types of motion before coming to rest. Most notably, the precession rate of the disk's axis of symmetry accelerates as the disk spins down. The rigid mirror is used to provide a suitable low-friction surface, with a slight concavity which keeps the spinning disk from "wandering" off a support surface.
An ordinary coin spun on a table, as with any disk spun on a relatively flat surface, exhibits essentially the same type of motion, but does not rotate for anywhere near as long as an Euler's Disk. Commercially available Euler's Disks provide a more effective demonstration of the phenomenon than more commonly found items, having an optimized aspect ratio and a precision polished, slightly rounded edge to maximize the spinning/rolling time.
Physics
A spinning/rolling disk ultimately comes to rest quite abruptly, the final stage of motion being accompanied by a whirring sound of rapidly increasing frequency. As the disk rolls, the point of rolling contact describes a circle that oscillates with a constant angular velocity 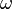 . If the motion is non-dissipative (frictionless),
. If the motion is non-dissipative (frictionless), 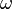 is constant, and the motion persists forever; this is contrary to observation, since
is constant, and the motion persists forever; this is contrary to observation, since 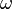 is not constant in real life situations. In fact, the precession rate of the axis of symmetry approaches a finite-time singularity modeled by a power law with exponent approximately −1/3 (depending on specific conditions).
is not constant in real life situations. In fact, the precession rate of the axis of symmetry approaches a finite-time singularity modeled by a power law with exponent approximately −1/3 (depending on specific conditions).
There are two conspicuous dissipative effects: rolling friction when the coin slips along the surface, and air drag from the resistance of air. Experiments show that rolling friction is mainly responsible for the dissipation and behavior—experiments in a vacuum show that the absence of air affects behavior only slightly, while the behavior (precession rate) depends systematically on coefficient of friction. In the limit of small angle (i.e. immediately before the disk stops spinning), air drag (specifically, viscous dissipation) is the dominant factor, but prior to this end stage, rolling friction is the dominant effect.
Steady motion with the disk center at rest
The behavior of a spinning disk whose center is at rest can be described as follows. Let the line from the center of the disk to the point of contact with the plane be called axis  . Since the center of the disk and the point of contact are instantaneously at rest (assuming there is no slipping) axis
. Since the center of the disk and the point of contact are instantaneously at rest (assuming there is no slipping) axis  is the instantaneous axis of rotation. The angular momentum is
is the instantaneous axis of rotation. The angular momentum is 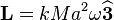 which holds for any thin, circularly symmetric disk with mass
which holds for any thin, circularly symmetric disk with mass 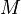 ;
;  for a disk with mass concentrated at the rim,
for a disk with mass concentrated at the rim, 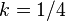 for a uniform disk (like Euler disk),
for a uniform disk (like Euler disk), 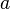 is the radius of the disk, and
is the radius of the disk, and 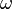 is the angular velocity along
is the angular velocity along  .
.
The contact force 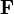 is
is 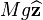 where
where 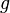 is the gravitational acceleration and
is the gravitational acceleration and 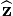 is the vertical axis pointing upwards. The torque about the center of mass is
is the vertical axis pointing upwards. The torque about the center of mass is 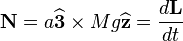 which we can rewrite as
which we can rewrite as 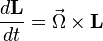 where
where 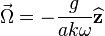 . We can conclude that both the angular momentum
. We can conclude that both the angular momentum 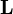 , and the disk are precessing about the vertical axis
, and the disk are precessing about the vertical axis 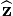 at rate Template:Repeat/0
at rate Template:Repeat/0
|
|
|
( |
Template:Repeat/0 At the same time 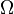 is the angular velocity of the point of contact with the plane. Let's define axis
is the angular velocity of the point of contact with the plane. Let's define axis 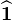 to lie along the symmetry axis of the disk and pointing downwards. Then it holds that
to lie along the symmetry axis of the disk and pointing downwards. Then it holds that 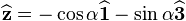 , where
, where 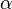 is the inclination angle of the disc with respect to the horizontal plane. The angular velocity can be thought of as composed of two parts
is the inclination angle of the disc with respect to the horizontal plane. The angular velocity can be thought of as composed of two parts 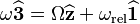 , where
, where 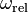 is the angular velocity of the disk along its symmetry axis. From the geometry we easily conclude that:
is the angular velocity of the disk along its symmetry axis. From the geometry we easily conclude that:
Plugging 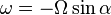 into equation (1) we finally get
into equation (1) we finally get
Template:Repeat/0
|
|
|
( |
Template:Repeat/0
As 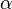 adiabatically approaches zero, the angular velocity of the point of contact
adiabatically approaches zero, the angular velocity of the point of contact 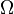 becomes very large, and one hears a high-frequency sound associated with the spinning disk. However, the rotation of the figure on the face of the coin, whose angular velocity is
becomes very large, and one hears a high-frequency sound associated with the spinning disk. However, the rotation of the figure on the face of the coin, whose angular velocity is  approaches zero. The total angular velocity
approaches zero. The total angular velocity 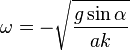 also vanishes as well as the total energy
also vanishes as well as the total energy
as 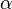 approaches zero. Here we have used the equation (2).
approaches zero. Here we have used the equation (2).
As 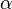 approaches zero the disk finally loses contact with the table and the disk then quickly settles on to the horizontal surface. One hears sound at a frequency
approaches zero the disk finally loses contact with the table and the disk then quickly settles on to the horizontal surface. One hears sound at a frequency 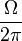 , which becomes dramatically higher until the sound abruptly ceases.
, which becomes dramatically higher until the sound abruptly ceases.
See also
 In Spanish: Disco de Euler para niños
In Spanish: Disco de Euler para niños