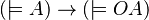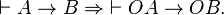Deontic logic facts for kids

Kids Encyclopedia Facts

Deontic logic is the field of philosophical logic that is concerned with obligation, permission, and related concepts. Alternatively, a deontic logic is a formal system that attempts to capture the essential logical features of these concepts. It can be used to formalize imperative logic, or directive modality in natural languages. Typically, a deontic logic uses OA to mean it is obligatory that A (or it ought to be (the case) that A), and PA to mean it is permitted (or permissible) that A, which is defined as 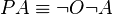$PA\equiv \neg O\neg A$ .

Note that in natural language, the statement "You may go to the zoo OR the park" should be understood as 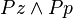$Pz\land Pp$ instead of 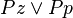$Pz\lor Pp$ , as both options are permitted by the statement; See Hans Kamp's paradox of free choice for more details.

When there are multiple agents involved in the domain of discourse, the deontic modal operator can be specified to each agent to express their individual obligations and permissions. For example, by using a subscript 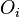$O_i$ for agent 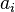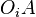$a_i$ , $O_iA$ means that "It is an obligation for agent 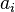$a_i$ (to bring it about/make it happen) that 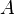$A$ ". Note that 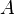$A$ could be stated as an action by another agent; One example is "It is an obligation for Adam that Bob doesn't crash the car", which would be represented as 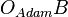$O_{Adam}B$ , where B="Bob doesn't crash the car".

Etymology
Standard deontic logic
- Semantics of standard deontic logic
- Anderson's deontic logic
Dyadic deontic logic
Other variations
History
- Early deontic logic
- Mally's first deontic logic and von Wright's first plausible deontic logic
Jørgensen's dilemma
See also

Etymology

The term deontic is derived from the Ancient Greek: δέον, romanized: déon (gen.: δέοντος, déontos), meaning "that which is binding or proper."

Standard deontic logic

In Georg Henrik von Wright's first system, obligatoriness and permissibility were treated as features of acts. Soon after this, it was found that a deontic logic of propositions could be given a simple and elegant Kripke-style semantics, and von Wright himself joined this movement. The deontic logic so specified came to be known as "standard deontic logic," often referred to as SDL, KD, or simply D. It can be axiomatized by adding the following axioms to a standard axiomatization of classical propositional logic:

(\models A) \rightarrow (\models OA)

O(A \rightarrow B) \rightarrow (OA \rightarrow OB)

OA\to PA

In English, these axioms say, respectively:

If A is a tautology, then it ought to be that A (necessitation rule N). In other words, contradictions are not permitted.
If it ought to be that A implies B, then if it ought to be that A, it ought to be that B (modal axiom K).
If it ought to be that A, then it is permitted that A (modal axiom D). In other words, if it's not permitted that A, then it's not obligatory that A.

FA, meaning it is forbidden that A, can be defined (equivalently) as 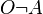$O \lnot A$ or $\lnot PA$ .

There are two main extensions of SDL that are usually considered. The first results by adding an alethic modal operator $\Box$ in order to express the Kantian claim that "ought implies can":

OA \to \Diamond A.

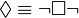where $\Diamond\equiv\lnot\Box\lnot$ . It is generally assumed that $\Box$ is at least a KT operator, but most commonly it is taken to be an S5 operator. In practical situations, obligations are usually assigned in anticipation of future events, in which case alethic possibilities can be hard to judge; Therefore, obligation assignments may be performed under the assumption of different conditions on different branches of timelines in the future, and past obligation assignments may be updated due to unforeseen developments that happened along the timeline.

The other main extension results by adding a "conditional obligation" operator O(A/B) read "It is obligatory that A given (or conditional on) B". Motivation for a conditional operator is given by considering the following ("Good Samaritan") case. It seems true that the starving and poor ought to be fed. But that the starving and poor are fed implies that there are starving and poor. By basic principles of SDL we can infer that there ought to be starving and poor! The argument is due to the basic K axiom of SDL together with the following principle valid in any normal modal logic:

\vdash A\to B\Rightarrow\ \vdash OA\to OB.

If we introduce an intensional conditional operator then we can say that the starving ought to be fed only on the condition that there are in fact starving: in symbols O(A/B). But then the following argument fails on the usual (e.g. Lewis 73) semantics for conditionals: from O(A/B) and that A implies B, infer OB.

Indeed, one might define the unary operator O in terms of the binary conditional one O(A/B) as 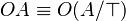$OA\equiv O(A/\top)$ , where $\top$ stands for an arbitrary tautology of the underlying logic (which, in the case of SDL, is classical).

Semantics of standard deontic logic

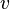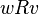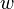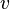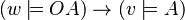The accessibility relation between possible world is interpreted as acceptability relations: $v$ is an acceptable world (viz. $wRv$ ) if and only if all the obligations in $w$ are fulfilled in $v$ (viz. $(w\models OA)\to (v\models A)$ ).

Anderson's deontic logic

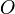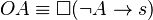Alan R. Anderson (1959) shows how to define $O$ in terms of the alethic operator $\Box$ and a deontic constant (i.e. 0-ary modal operator) $s$ standing for some sanction (i.e. bad thing, prohibition, etc.): $OA\equiv\Box(\lnot A\to s)$ . Intuitively, the right side of the biconditional says that A's failing to hold necessarily (or strictly) implies a sanction.

In addition to the usual modal axioms (necessitation rule N and distribution axiom K) for the alethic operator $\Box$ , Anderson's deontic logic only requires one additional axiom for the deontic constant $s$ : $\neg \Box s\equiv \Diamond \neg s$ , which means that there is alethically possible to fulfill all obligations and avoid the sanction. This version of the Anderson's deontic logic is equivalent to SDL.

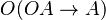However, when modal axiom T is included for the alethic operator ( $\Box A\to A$ ), it can be proved in Anderson's deontic logic that $O(OA \to A)$ , which is not included in SDL. Anderson's deontic logic inevitably couples the deontic operator 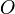$O$ with the alethic operator $\Box$ , which can be problematic in certain cases.

Dyadic deontic logic

An important problem of deontic logic is that of how to properly represent conditional obligations, e.g. If you smoke (s), then you ought to use an ashtray (a). It is not clear that either of the following representations is adequate:

O(\mathrm{smoke} \rightarrow \mathrm{ashtray})

\mathrm{smoke} \rightarrow O(\mathrm{ashtray})

Under the first representation it is vacuously true that if you commit a forbidden act, then you ought to commit any other act, regardless of whether that second act was obligatory, permitted or forbidden (Von Wright 1956, cited in Aqvist 1994). Under the second representation, we are vulnerable to the gentle murder paradox, where the plausible statements (1) if you murder, you ought to murder gently, (2) you do commit murder, and (3) to murder gently you must murder imply the less plausible statement: you ought to murder. Others argue that must in the phrase to murder gently you must murder is a mistranslation from the ambiguous English word (meaning either implies or ought). Interpreting must as implies does not allow one to conclude you ought to murder but only a repetition of the given you murder. Misinterpreting must as ought results in a perverse axiom, not a perverse logic. With use of negations one can easily check if the ambiguous word was mistranslated by considering which of the following two English statements is equivalent with the statement to murder gently you must murder: is it equivalent to if you murder gently it is forbidden not to murder or if you murder gently it is impossible not to murder ?

Some deontic logicians have responded to this problem by developing dyadic deontic logics, which contain binary deontic operators:

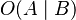O(A \mid B)

means it is obligatory that A, given B

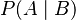P(A \mid B)

means it is permissible that A, given B.

(The notation is modeled on that used to represent conditional probability.) Dyadic deontic logic escapes some of the problems of standard (unary) deontic logic, but it is subject to some problems of its own.

Other variations

Many other varieties of deontic logic have been developed, including non-monotonic deontic logics, paraconsistent deontic logics, and dynamic deontic logics.

History

Early deontic logic

Philosophers from the Indian Mimamsa school to those of Ancient Greece have remarked on the formal logical relations of deontic concepts and philosophers from the late Middle Ages compared deontic concepts with alethic ones.

In his Elementa juris naturalis (written between 1669 and 1671), Gottfried Wilhelm Leibniz notes the logical relations between the licitum (permitted), the illicitum (prohibited), the debitum (obligatory), the, and the indifferens (facultative) are equivalent to those between the possibile, the impossibile, the necessarium, and the contingens respectively.

Mally's first deontic logic and von Wright's first plausible deontic logic

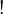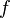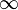Ernst Mally, a pupil of Alexius Meinong, was the first to propose a formal system of deontic logic in his Grundgesetze des Sollens (1926) and he founded it on the syntax of Whitehead's and Russell's propositional calculus. Mally's deontic vocabulary consisted of the logical constants $\cup$ and $\cap$ , unary connective $!$ , and binary connectives $f$ and $\infty$ .

* Mally read

!A

as "A ought to be the case".
* He read

A f B

as "A requires B" .
* He read

A \infty B

as "A and B require each other."
* He read

\cup

as "the unconditionally obligatory" .
* He read

\cap

as "the unconditionally forbidden".

Mally defined 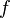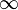$f$ , $\infty$ , and $\cap$ as follows:

Def.

f. A f B = A \rightarrow !B

Def.

\infty. A \infty B = (A f B) \& (B f A)

Def.

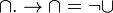
\cap.\rightarrow \cap=\lnot\cup

Mally proposed five informal principles:

(i) If A requires B and if B requires C, then A requires C.
(ii) If A requires B and if A requires C, then A requires B and C.
(iii) A requires B if and only if it is obligatory that if A then B.
(iv) The unconditionally obligatory is obligatory.
(v) The unconditionally obligatory does not require its own negation.

He formalized these principles and took them as his axioms:

\rightarrow ((A f B) \& (B \rightarrow C)) \rightarrow (A f C)

II.

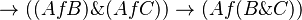
\rightarrow ((A f B) \& (A f C)) \rightarrow (A f (B \& C))

III.

\rightarrow (A f B) \leftrightarrow !(A \rightarrow B)

IV.

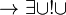
\rightarrow \exists \cup ! \cup

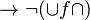
\rightarrow \lnot (\cup f \cap)

From these axioms Mally deduced 35 theorems, many of which he rightly considered strange. Karl Menger showed that $!A \leftrightarrow A$ is a theorem and thus that the introduction of the ! sign is irrelevant and that A ought to be the case if A is the case. After Menger, philosophers no longer considered Mally's system viable. Gert Lokhorst lists Mally's 35 theorems and gives a proof for Menger's theorem at the Stanford Encyclopedia of Philosophy under Mally's Deontic Logic.

The first plausible system of deontic logic was proposed by G. H. von Wright in his paper Deontic Logic in the philosophical journal Mind in 1951. (Von Wright was also the first to use the term "deontic" in English to refer to this kind of logic although Mally published the German paper Deontik in 1926.) Since the publication of von Wright's seminal paper, many philosophers and computer scientists have investigated and developed systems of deontic logic. Nevertheless, to this day deontic logic remains one of the most controversial and least agreed-upon areas of logic. G. H. von Wright did not base his 1951 deontic logic on the syntax of the propositional calculus as Mally had done, but was instead influenced by alethic modal logics, which Mally had not benefited from. In 1964, von Wright published A New System of Deontic Logic, which was a return to the syntax of the propositional calculus and thus a significant return to Mally's system. (For more on von Wright's departure from and return to the syntax of the propositional calculus, see Deontic Logic: A Personal View and A New System of Deontic Logic, both by Georg Henrik von Wright.) G. H. von Wright's adoption of the modal logic of possibility and necessity for the purposes of normative reasoning was a return to Leibniz.

Although von Wright's system represented a significant improvement over Mally's, it raised a number of problems of its own. For example, Ross's paradox applies to von Wright's deontic logic, allowing us to infer from "It is obligatory that the letter is mailed" to "It is obligatory that either the letter is mailed or the letter is burned", which seems to imply it is permissible that the letter is burned. The Good Samaritan paradox also applies to his system, allowing us to infer from "It is obligatory to nurse the man who has been robbed" that "It is obligatory that the man has been robbed". Another major source of puzzlement is Chisholm's paradox. There is no formalisation in von Wright's system of the following claims that allows them to be both jointly satisfiable and logically independent:

It ought to be that Jones goes (to the assistance of his neighbors).
It ought to be that if Jones goes, then he tells them he is coming.
If Jones doesn't go, then he ought not tell them he is coming.
Jones doesn't go

Jørgensen's dilemma

Deontic logic faces Jørgensen's dilemma. This problem is best seen as a trilemma. The following three claims are incompatible:

Logical inference requires that the elements (premises and conclusions) have truth-values
Normative statements do not have truth-values
There are logical inferences between normative statements

Responses to this problem involve rejecting one of the three premises.

The input/output logics reject the first premise. They provide inference mechanism on elements without presupposing that these elements have truth-values.
Alternatively, one can deny the second premise. One way to do this is to distinguish between the norm itself and a proposition about the norm. According to this response, only the proposition about the norm (as is the case for Standard Deontic Logic) has a truth-value. For example, it may be hard to assign a truth-value to the argument "Take all the books off the table!", but 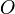$O$ ("take all the books off the table"), which means "It is obligatory to take all the books off the table", can be assigned a truth-value, because it is in the indicative mood.
Finally, one can deny the third premise. But this is to deny that there is a logic of norms worth investigating.

Deontic logic facts for kids

Contents

Etymology

Standard deontic logic

Semantics of standard deontic logic

Anderson's deontic logic

Dyadic deontic logic

Other variations

History

Early deontic logic

Mally's first deontic logic and von Wright's first plausible deontic logic

Jørgensen's dilemma

See also